Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T19:52:46.391Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady dynamics of rapid perching manoeuvres

Published online by Cambridge University Press:  13 February 2015

Delyle T. Polet ,
David E. Rival  and
Gabriel D. Weymouth
Delyle T. Polet
Affiliation:
Department of Mechanical Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada
David E. Rival
Affiliation:
Department of Mechanical Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada Department of Mechanical and Materials Engineering, Queen’s University, Kingston, ON K7L 3N6, Canada
Gabriel D. Weymouth*
Affiliation:
Southampton Marine and Maritime Institute, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A perching bird is able to rapidly decelerate while maintaining lift and control, but the underlying aerodynamic mechanism is poorly understood. In this work we perform a study on a simultaneously decelerating and pitching aerofoil section to increase our understanding of the unsteady aerodynamics of perching. We first explore the problem analytically, developing expressions for the added-mass and circulatory forces arising from boundary-layer separation on a flat-plate aerofoil. 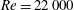Next, we study the model problem through a detailed series of experiments at $\mathit{Re}=22\,000$ and two-dimensional simulations at $\mathit{Re}=2000$. Simulated vorticity fields agree with particle image velocimetry measurements, showing the same wake features and vorticity magnitudes. Peak lift and drag forces during rapid perching are measured to be more than 10 times the quasi-steady values. The majority of these forces can be attributed to added-mass energy transfer between the fluid and aerofoil, and to energy lost to the fluid by flow separation at the leading and trailing edges. Thus, despite the large angles of attack and decreasing flow velocity, this simple pitch-up manoeuvre provides a means through which a perching bird can maintain high lift and drag simultaneously while slowing to a controlled stop.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 323 - 341
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baik, Y., Bernal, L., Granlund, K. & Ol, M. 2012 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 709, 37–68.CrossRefGoogle Scholar
Berg, A. M. & Biewener, A. A. 2010 Wing and body kinematics of takeoff and landing flight in the pigeon (Columbia livia). J. Expl Biol. 213, 1651–1658.Google Scholar
Carruthers, A. C., Thomas, A. L. R. & Taylor, G. K. 2007 Automatic aeroelastic devices in the wings of a steppe eagle Aquila nipalensis . J. Expl Biol. 210 (23), 4136–4149.Google Scholar
Carruthers, A. C., Thomas, A. L. R., Walker, S. M. & Taylor, G. K. 2010 Mechanics and aerodynamics of perching manoeuvres in a large bird of prey. Aeronaut. J. 114 (1161), 673–680.Google Scholar
Doyle, C. E., Bird, J. J., Isom, T. A., Johnson, C. J., Kallman, J. C., Simpson, J. A., King, R. J., Abbott, J. J. & Minor, M. A.2011 Avian-inspired passive perching mechanism for robotic rotorcraft. In IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2011, pp. 4975–4980.Google Scholar
Garmann, D. J., Visbal, M. & Orkwis, P. D. 2013 Three-dimensional flow structure and aerodynamic loading on a revolving wing. Phys. Fluids 25, 034101.Google Scholar
Green, P. R. & Cheng, P. 1998 Variation in kinematics and dynamics of the landing flights of pigeons on a novel perch. J. Expl Biol. 201 (24), 3309–3316.CrossRefGoogle ScholarPubMed
von Kármán, T. & Sears, W. R. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5, 379–390.CrossRefGoogle Scholar
Maertens, A. P. & Weymouth, G. D. 2015 Accurate Cartesian-grid simulations of near-body flows at intermediate Reynolds numbers. Comput. Meth. Appl. Mech. Engng 283, 106–129.Google Scholar
McCroskey, W. J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14 (1), 285–311.CrossRefGoogle Scholar
Milne-Thomson, L. M. 1968 Theoretical Hydrodynamics, 5th edn. Macmillan.Google Scholar
Moore, J., Cory, R. & Tedrake, R. 2014 Robust post-stall perching with a simple fixed-wing glider using LQR-trees. Bioinspir. Biomim. 9 (2), 025013.CrossRefGoogle ScholarPubMed
Ol, M. V., Bernal, L., Kang, C. K. & Shyy, W. 2009 Shallow and deep dynamic stall for flapping low Reynolds number airfoils. Exp. Fluids 46, 883–901.CrossRefGoogle Scholar
Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99 (1), 129–144.CrossRefGoogle Scholar
Pitt Ford, C. W. & Babinsky, H. 2013 Lift and the leading edge vortex. J. Fluid Mech. 720, 280–313.Google Scholar
Provini, P., Tobalske, B. W., Crandell, K. E. & Abourachid, A. 2014 Transition from wing to leg forces during landing in birds. J. Expl Biol. 217, 2659–2666.Google Scholar
Raffel, M., Willert, C., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide, 2nd edn. Springer.Google Scholar
Reich, G., Wojnar, O. & Albertani, R. 2009 Aerodynamic performance of a notional perching MAV design. In Proceedings of the 47th AIAA Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics. Article ID: 2009-63.Google Scholar
Saffman, P. G. & Szeto, R. 1980 Equilibrium shapes of a pair of equal uniform vortices. Phys. Fluids 23 (12), 2339–2342.CrossRefGoogle Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496.Google Scholar
Wagner, H. 1925 Über die Entstehung des dynamischen Auftriebes von Tragflügeln. Z. Angew. Math. Mech. 5 (1), 17–35.CrossRefGoogle Scholar
Weymouth, G. D. & Triantafyllou, M. S. 2012 Global vorticity shedding for a shrinking cylinder. J. Fluid Mech. 702, 470–487.Google Scholar
Weymouth, G. D. & Triantafyllou, M. S. 2013 Ultra-fast escape of a deformable jet-propelled body. J. Fluid Mech. 721, 367–385.Google Scholar
Weymouth, G. D. & Yue, D. K. P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid–body interaction problems. J. Comput. Phys. 230 (16), 6233–6247.Google Scholar
Wibawa, M. S., Steele, S. C., Dahl, J. M., Rival, D. E., Weymouth, G. D. & Triantafyllou, M. S. 2012 Global vorticity shedding for a vanishing wing. J. Fluid Mech. 695, 112–134.Google Scholar
Xia, X. & Mohseni, K. 2013 Lift evaluation of a two-dimensional pitching flat plate. Phys. Fluids 25, 091901.CrossRefGoogle Scholar