Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-01T22:25:15.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Unstable jets generated by a sphere descending in a very strongly stratified fluid

Published online by Cambridge University Press:  20 March 2019

Shinsaku Akiyama ,
Yusuke Waki ,
Shinya Okino Open the ORCID record for Shinya Okino [Opens in a new window]  and
Hideshi Hanazaki Open the ORCID record for Hideshi Hanazaki [Opens in a new window]
Shinsaku Akiyama
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto Daigaku-Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
Yusuke Waki
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto Daigaku-Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
Shinya Okino*
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto Daigaku-Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
Hideshi Hanazaki
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto Daigaku-Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow around a sphere descending at constant speed in a very strongly stratified fluid (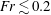$Fr\lesssim 0.2$) is investigated by the shadowgraph method and particle image velocimetry. Unlike the flow under moderately strong stratification (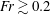$Fr\gtrsim 0.2$), which supports a thin cylindrical jet, the flow generates an unstable jet, which often develops into turbulence. The transition from a stable jet to an unstable jet occurs for a sufficiently low Froude number 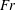$Fr$ that satisfies 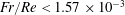$Fr/Re<1.57\times 10^{-3}$. The Froude number 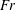$Fr$ here is in the range of 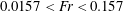$0.0157<Fr<0.157$ or lower, while the Reynolds number 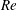$Re$ is in the range of 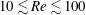$10\lesssim Re\lesssim 100$ for which the homogeneous fluid shows steady and axisymmetric flows. Since the radius of the jet can be estimated by the primitive length scale of the stratified fluid, i.e. $l_{\unicode[STIX]{x1D708}}^{\ast }=\sqrt{\unicode[STIX]{x1D708}^{\ast }/N^{\ast }}$ or 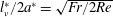$l_{\unicode[STIX]{x1D708}}^{\ast }/2a^{\ast }=\sqrt{Fr/2Re}$, this predicts that the jet becomes unstable when it becomes thinner than approximately 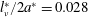$l_{\unicode[STIX]{x1D708}}^{\ast }/2a^{\ast }=0.028$, where 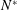$N^{\ast }$ is the Brunt–Väisälä frequency, 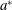$a^{\ast }$ the radius of the sphere and 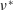$\unicode[STIX]{x1D708}^{\ast }$ the kinematic viscosity of the fluid. The instability begins when the boundary-layer thickness becomes thin, and the disturbances generated by shear instabilities would be transferred into the jet. When the flow is marginally unstable, two unstable states, i.e. a meandering jet and a turbulent jet, can appear. The meandering jet is thin with a high vertical velocity, while the turbulent jet is broad with a much smaller velocity. The meandering jet may persist for a long time, or develop into a turbulent jet in a short time. When the instability is sufficiently strong, only the turbulent jet could be observed.

JFM classification

Geophysical and Geological Flows: Internal waves Wakes/Jets: Jets Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 26 - 44
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abaid, N., Adalsteinsson, D., Agyapong, A. & McLaughlin, R. M. 2004 An internal splash: levitation of falling spheres in stratified fluids. Phys. Fluids 16, 1567–1580.Google Scholar
Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.Google Scholar
D’Asaro, E. A. 2003 Performance of autonomous Lagrangian floats. J. Atmos. Ocean. Technol. 20, 896–911.Google Scholar
Daviero, G. J., Roberts, P. J. W. & Maile, M. 2001 Refractive index matching in large-scale stratified experiments. Exp. Fluids 31, 119–126.Google Scholar
Doostmohammadi, A., Dabiri, S. & Ardekani, A. M. 2014 A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J. Fluid Mech. 750, 5–32.Google Scholar
Fortuin, J. M. H. 1960 Theory and application of two supplementary methods of constructing density gradient columns. J. Polym. Sci. 44, 505–515.Google Scholar
Gibson, C. H. 1980 Fossil temperature, salinity, and vorticity turbulence in the ocean. In Marine Turbulence (ed. Nihoul, J.), pp. 221–257. Elsevier.Google Scholar
Hanazaki, H., Kashimoto, K. & Okamura, T. 2009a Jets generated by a sphere moving vertically in a stratified fluid. J. Fluid Mech. 638, 173–197.Google Scholar
Hanazaki, H., Konishi, H. & Okamura, T. 2009b Schmidt-number effects of the flow past a sphere moving vertically in a stratified diffusive fluid. Phys. Fluids 21, 026602.Google Scholar
Hanazaki, H., Nakamura, S. & Yoshikawa, H. 2015 Numerical simulation of jets generated by a sphere moving vertically in a stratified fluid. J. Fluid Mech. 765, 424–451.Google Scholar
MacIntyre, S. A., Alldredge, A. L. & Gottschalk, C. C. 1995 Accumulation of marine show at density discontinuities in the water column. Limnol. Oceanogr. 40 (3), 449–468.Google Scholar
Marsay, C. M., Sanders, R. J., Henson, S. A., Pabortsava, K., Achterberg, E. P. & Lampitt, R. S. 2015 Attenuation of sinking particulate organic carbon flux through the mesopelagic ocean. Proc. Natl Acad. Sci. USA 112 (4), 1089–1094.Google Scholar
McDougall, T. J. 1979 On the elimination of refractive-index variations in turbulent density-stratified liquid flows. J. Fluid Mech. 93, 83–96.Google Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 The internal wave pattern produced by a sphere moving vertically in a density stratified liquid. J. Fluid Mech. 30 (3), 489–495.Google Scholar
Ochoa, J. L. & Van Woert, M. L.1977 Flow visualization of boundary layer separation in a stratified fluid. Unpublished Report. Scripps Institution of Oceanography, 28.Google Scholar
Okino, S., Akiyama, S. & Hanazaki, H. 2017 Velocity distribution around a sphere descending in a linearly stratified fluid. J. Fluid Mech. 826, 759–780.Google Scholar
Prairie, J. C., Ziervogel, K., Camassa, R., McLaughlin, R. M., White, B. L., Dewald, C. & Arnosti, C. 2015 Delayed settling of marine snow: effects of density gradient and particle properties and implications for carbon cycling. Mar. Chem. 175, 28–38.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.Google Scholar
Torres, C. R., Hanazaki, H., Ochoa, J., Castillo, J. & Van Woert, M. 2000 Flow past a sphere moving vertically in a stratified diffusive fluid. J. Fluid Mech. 417, 211–236.Google Scholar
Van Dyke, M. 1982 An Album of Fluid Motion. Parabolic Press.Google Scholar
Yick, K. Y., Torres, C. R., Peacock, T. & Stocker, R. 2009 Enhanced drag of a sphere settling in a stratified fluid at small Reynolds numbers. J. Fluid Mech. 632, 49–68.Google Scholar