Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T02:44:52.833Z Has data issue: false hasContentIssue false
  • English
  • Français

The universal aspect ratio of vortices in rotating stratified flows: experiments and observations

Published online by Cambridge University Press:  25 May 2012

Oriane Aubert ,
Michael Le Bars ,
Patrice Le Gal  and
Philip S. Marcus
Oriane Aubert*
Affiliation:
Institut de Recherche sur les Phénomènes Hors Equilibre, UMR 7342, CNRS and Aix-Marseille Université, 49 rue F. Joliot Curie, 13384 Marseille, CEDEX 13, France
Michael Le Bars
Affiliation:
Institut de Recherche sur les Phénomènes Hors Equilibre, UMR 7342, CNRS and Aix-Marseille Université, 49 rue F. Joliot Curie, 13384 Marseille, CEDEX 13, France
Patrice Le Gal
Affiliation:
Institut de Recherche sur les Phénomènes Hors Equilibre, UMR 7342, CNRS and Aix-Marseille Université, 49 rue F. Joliot Curie, 13384 Marseille, CEDEX 13, France
Philip S. Marcus
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We validate a new law for the aspect ratio of vortices in a rotating, stratified flow, where 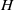and 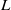are the vertical half-height and horizontal length scale of the vortices. The aspect ratio depends not only on the Coriolis parameter 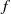and buoyancy (or Brunt–Väisälä) frequency 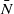of the background flow, but also on the buoyancy frequency 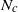within the vortex and on the Rossby number 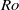of the vortex, such that 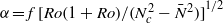. This law for is obeyed precisely by the exact equilibrium solution of the inviscid Boussinesq equations that we show to be a useful model of our laboratory vortices. The law is valid for both cyclones and anticyclones. Our anticyclones are generated by injecting fluid into a rotating tank filled with linearly stratified salt water. In one set of experiments, the vortices viscously decay while obeying our law for , which decreases over time. In a second set of experiments, the vortices are sustained by a slow continuous injection. They evolve more slowly and have larger 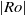while still obeying our law for . The law for is not only validated by our experiments, but is also shown to be consistent with observations of the aspect ratios of Atlantic meddies and Jupiter’s Great Red Spot and Oval BA. The relationship for is derived and examined numerically in a companion paper by Hassanzadeh, Marcus & Le Gal (J. Fluid Mech., vol. 706, 2012, pp. 46–57).

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 34 - 45
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Antipov, S. V., Nezlin, M. V., Snezhkin, E. N. & Trubinikov, A. S. 1986 Rossby autosoliton and stationary model of the Jovian Great Red Spot. Nature 323, 238–240.CrossRefGoogle Scholar
2. Armi, L., Hebert, D., Oakey, N., Price, J. F., Richardson, P. L., Rossby, H. T. & Ruddick, B. 1988 The history and decay of a Mediterranean salt lens. Nature 333, 649–651.CrossRefGoogle Scholar
3. Banfield, D., Gierasch, P. J., Bell, M., Ustinov, E., Ingersoll, A. P., Vasada, A. R., West, R. A. & Belton, M. J. S. 1988 Jupiter’s cloud structure from Galileo imaging data. Icarus 135, 230–250.CrossRefGoogle Scholar
4. Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.CrossRefGoogle Scholar
5. Bush, J. M. W. & Woods, A. W. 1999 Vortex generation by line plumes in a rotating stratified fluid. J. Fluid Mech. 388, 289–313.CrossRefGoogle Scholar
6. Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22, 179–263.CrossRefGoogle Scholar
7. Dritschel, D. G., de la Torre Juarez, M. & Ambaum, M. H. P. 1999 The three-dimensional vortical nature of atmospheric and oceanic turbulent flows. Phys. Fluids 11, 1512–1520.CrossRefGoogle Scholar
8. Fletcher, L. N., Orton, G. S., Mousis, O., Yanamandra-Fisher, P., Parrish, P. D., Irwin, P. G. J., Fisher, B. M., Vanzi, L., Fujiyoshi, T., Fuse, T., SImon-Miller, A. A., Edkins, E., Hayward, T. L. & De Buizer, J. 2010 Thermal structure and composition of Jupiter’s Great Red Spot from high-resolution thermal imaging. Icarus 208, 306–318.CrossRefGoogle Scholar
9. Gill, A. E. 1981 Homogeneous intrusions in a rotating stratified fluid. J. Fluid Mech. 103, 275–295.CrossRefGoogle Scholar
10. Griffiths, R. W. & Linden, P. F. 1981 The stability of vortices in a rotating, stratified fluid. J. Fluid Mech. 105, 283–316.CrossRefGoogle Scholar
11. Hassanzadeh, P., Marcus, P. S. & Le Gal, P. 2012 The universal aspect ratio of vortices in rotating stratified flows: theory and simulation. J. Fluid Mech. 706, 46–57.CrossRefGoogle Scholar
12. Hebert, D., Oakley, N. & Ruddick, B. 1990 Evolution of a Mediterranean salt lens: scalar properties. J. Phys. Oceanogr. 20, 1468–1483.2.0.CO;2>CrossRefGoogle Scholar
13. Hedstrom, K. & Armi, L. 1988 An experimental study of homogeneous lenses in a stratified rotating fluid. J. Fluid Mech. 191, 535–556.CrossRefGoogle Scholar
14. Marcus, P. S. 1993 Jupiter’s Great Red Spot and other vortices. Annu. Rev. Astron. Astrophys. 31, 523–573.CrossRefGoogle Scholar
15. McWilliams, J. C. 1985 Submesoscale, coherent vortices in the ocean. Rev. Geophys. 23, 165–183.CrossRefGoogle Scholar
16. Meunier, P. & Leweke, T. 2003 Analysis and treatment of errors due to high gradients in particle image velocimetry. Exp. Fluids 35, 408–421.CrossRefGoogle Scholar
17. Morales-Juberias, R., Sanchez-Lavega, A. & Dowling, T. E. 2003 EPIC simulations of the merger of Jupiter’s White Ovals BE and FA: altitude-dependent behavior. Icarus 166, 63–74.CrossRefGoogle Scholar
18. Nof, D. 1981 On the -induced movement of isolated baroclinic eddies. J. Phys. Oceanogr. 11, 1662–1672.2.0.CO;2>CrossRefGoogle Scholar
19. Oster, G. 1965 Density gradients. Sci. Am. 213, 70–76.CrossRefGoogle Scholar
20. de Pater, I., Wong, M. H., Marcus, P. S., Luszcz-Cook, S., Adamkovics, M., Conrad, A., Asay-Davis, X. & Go, C. 2010 Persistent rings in and around Jupiter’s anticyclones: Observations and theory. Icarus 210, 742–762.CrossRefGoogle Scholar
21. Pingree, R. D. & Le Cann, B. 1993 Structure of a meddy (Bobby 92) southeast of the Azores. Deep-Sea Res. (I) 40, 2077–2103.CrossRefGoogle Scholar
22. Reinaud, J. N., Dritschel, D. G. & Koudella, C. R. 2003 The shape of vortices in quasi-geostrophic turbulence. J. Fluid Mech. 474, 175–192.CrossRefGoogle Scholar
23. Schlutz Tokos, K. & Rossby, T. 1990 Kinematics and dynamics of a Mediterranean salt lens. J. Phys. Oceanogr. 21, 879–892.2.0.CO;2>CrossRefGoogle Scholar
24. Shetty, S. & Marcus, P. S. 2010 Changes in Jupiter’s Great Red Spot(1979–2006) and Oval BA (2000–2006). Icarus 210, 182–201.CrossRefGoogle Scholar
25. Sommeria, J., Meyers, S. D. & Swinney, H. L. 1988 Laboratory simulation of Jupiter’s Great Red Spot. Nature 331, 689–693.CrossRefGoogle Scholar
26. Tychensky, A. & Carton, X. 1998 Hydrological and dynamical characterization of meddies in the Azores region: a paradigm for baroclinic vortex dynamics. J. Geophys. Res. 103, 25061–25079.CrossRefGoogle Scholar
Supplementary material: PDF

Aubert et al. supplementary material

Appendix

Download Aubert et al. supplementary material(PDF)
PDF 190.4 KB