Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T16:44:25.120Z Has data issue: false hasContentIssue false
  • English
  • Français

The transition to turbulence in shock-driven mixing: effects of Mach number and initial conditions

Published online by Cambridge University Press:  24 May 2019

Mohammad Mohaghar ,
John Carter ,
Gokul Pathikonda  and
Devesh Ranjan Open the ORCID record for Devesh Ranjan [Opens in a new window]
Mohammad Mohaghar
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
John Carter
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
Gokul Pathikonda
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
Devesh Ranjan*
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of incident shock strength on the mixing transition in the Richtmyer–Meshkov instability (RMI) are experimentally investigated using simultaneous density–velocity measurements. This effort uses a shock with an incident Mach number of 1.9, in concert with previous work at Mach 1.55 (Mohaghar et al., J. Fluid Mech., vol. 831, 2017 pp. 779–825) where each case is followed by a reshock wave. Single- and multi-mode interfaces are used to quantify the effect of initial conditions on the evolution of the RMI. The interface between light and heavy gases (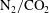$\text{N}_{2}/\text{CO}_{2}$, Atwood number, 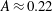$A\approx 0.22$; amplitude to wavelength ratio of 0.088) is created in an inclined shock tube at 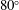$80^{\circ }$ relative to the horizontal, resulting in a predominantly single-mode perturbation. To investigate the effects of initial perturbations on the mixing transition, a multi-mode inclined interface is also created via shear and buoyancy superposed on the dominant inclined perturbation. The evolution of mixing is investigated via the density fields by computing mixed mass and mixed-mass thickness, along with mixing width, mixedness and the density self-correlation (DSC). It is shown that the amount of mixing is dependent on both initial conditions and incident shock Mach number. Evolution of the density self-correlation is discussed and the relative importance of different DSC terms is shown through fields and spanwise-averaged profiles. The localized distribution of vorticity and the development of roll-up features in the flow are studied through the evolution of interface wrinkling and length of the interface edge, which indicate that the vorticity concentration shows a strong dependence on the Mach number. The contribution of different terms in the Favre-averaged Reynolds stress is shown, and while the mean density-velocity fluctuation correlation term, 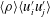$\langle \unicode[STIX]{x1D70C}\rangle \langle u_{i}^{\prime }u_{j}^{\prime }\rangle$, is dominant, a high dependency on the initial condition and reshock is observed for the turbulent mass-flux term. Mixing transition is analysed through two criteria: the Reynolds number (Dimotakis, J. Fluid Mech., vol. 409, 2000, pp. 69–98) for mixing transition and Zhou (Phys. Plasmas, vol. 14 (8), 2007, 082701 for minimum state) and the time-dependent length scales (Robey et al., Phys. Plasmas, vol. 10 (3), 2003, 614622; Zhou et al., Phys. Rev. E, vol. 67 (5), 2003, 056305). The Reynolds number threshold is surpassed in all cases after reshock. In addition, the Reynolds number is around the threshold range for the multi-mode, high Mach number case (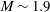$M\sim 1.9$) before reshock. However, the time-dependent length-scale threshold is surpassed by all cases only at the latest time after reshock, while all cases at early times after reshock and the high Mach number case at the latest time before reshock fall around the threshold. The scaling analysis of the turbulent kinetic energy spectra after reshock at the latest time, at which mixing transition analysis suggests that an inertial range has formed, indicates power scaling of 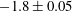$-1.8\pm 0.05$ for the low Mach number case and 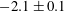$-2.1\pm 0.1$ for the higher Mach number case. This could possibly be related to the high anisotropy observed in this flow resulting from strong, large-scale streamwise fluctuations produced by large-scale shear.

JFM classification

Compressible Flows: Shock waves Instability: Transition to turbulence Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 595 - 635
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnett, D. 2000 The role of mixing in astrophysics. Astrophys. J. Suppl. Ser. 127 (2), 213–217.10.1086/313364Google Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.10.1017/jfm.2012.8Google Scholar
Balakumar, B. J., Orlicz, G. C., Tomkins, C. D. & Prestridge, K. P. 2008 Dependence of growth patterns and mixing width on initial conditions in Richtmyer–Meshkov unstable fluid layers. Phys. Scr. 2008 (T132), 014013.Google Scholar
Besnard, D., Harlow, F. H., Rauenzahn, R. M. & Zemach, C.1992 Turbulence transport equations for variable-density turbulence and their relationship to two-field models. Tech. Rep. Los Alamos National Lab., lA-12303-MS.10.2172/7271399Google Scholar
Bonazza, R. & Sturtevant, B. 1996 X-ray measurements of growth rates at a gas interface accelerated by shock waves. Phys. Fluids 8 (9), 2496–2512.10.1063/1.869033Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34 (1), 445–468.10.1146/annurev.fluid.34.090101.162238Google Scholar
Canny, J. 1986 A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. (6), 679–698.10.1109/TPAMI.1986.4767851Google Scholar
Champagne, F. H., Harris, V. G. & Corrsin, S. 1970 Experiments on nearly homogeneous turbulent shear flow. J. Fluid Mech. 41 (1), 81–139.10.1017/S0022112070000538Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.10.1017/S0022112099007946Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.10.1146/annurev.fluid.36.050802.122015Google Scholar
Erez, L., Sadot, O., Oron, D., Erez, G., Levin, L. A., Shvarts, D. & Ben-Dor, G. 2000 Study of the membrane effect on turbulent mixing measurements in shock tubes. Shock Waves 10 (4), 241–251.10.1007/s001930000053Google Scholar
Fries, D., Ochs, B., Saha, A., Ranjan, D. & Menon, S. 2019 Flame speed characteristics of turbulent expanding flames in a rectangular channel. Combust. Flame 199C, 1–13.10.1016/j.combustflame.2018.10.008Google Scholar
Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.10.1017/S0022112006009475Google Scholar
Jacobs, J. W. & Sheeley, J. M. 1996 Experimental study of incompressible Richtmyer–Meshkov instability. Phys. Fluids 8 (2), 405–415.10.1063/1.868794Google Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9 (10), 3078–3085.10.1063/1.869416Google Scholar
Kerstein, A. R. 1991 Linear-eddy modelling of turbulent transport. Part 6. Microstructure of diffusive scalar mixing fields. J. Fluid Mech. 231, 361–394.10.1017/S0022112091003439Google Scholar
Latini, M., Schilling, O. & Don, W. 2007 Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer–Meshkov instability. J. Comput. Phys. 221 (2), 805–836.10.1016/j.jcp.2006.06.051Google Scholar
Leinov, E., Malamud, G., Elbaz, Y., Levin, L. A., Ben-Dor, G., Shvarts, D. & Sadot, O. 2009 Experimental and numerical investigation of the Richtmyer–Meshkov instability under re-shock conditions. J. Fluid Mech. 626, 449–475.10.1017/S0022112009005904Google Scholar
Lindl, J. D., Landen, O., Edwards, J., Moses, E. D.& Team NIC 2014 Review of the National Ignition Campaign 2009–2012. Phys. Plasmas 21 (2), 020501.10.1063/1.4865400Google Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.10.1017/S0022112008001481Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2012 Transition to turbulence in shock-driven mixing: a Mach number study. J. Fluid Mech. 690, 203–226.10.1017/jfm.2011.425Google Scholar
Malm, H., Sparr, G., Hult, J. & Kaminski, C. F. 2000 Nonlinear diffusion filtering of images obtained by planar laser-induced fluorescence spectroscopy. J. Opt. Soc. Am. A 17 (12), 2148–2156.10.1364/JOSAA.17.002148Google Scholar
Marble, F. E., Hendricks, G. J. & Zukoski, E. E. 1989 Progress toward shock enhancement of supersonic combustion processes. In Turbulent Reactive Flows, pp. 932–950. Springer.10.1007/978-1-4613-9631-4_43Google Scholar
McFarland, J., Greenough, J. & Ranjan, D. 2014a Simulations and analysis of the reshocked inclined interface Richtmyer–Meshkov instability for linear and nonlinear interface perturbations. Trans. ASME J. Fluids Engng 136 (7), 071203.10.1115/1.4026858Google Scholar
McFarland, J., Reilly, D., Creel, S., McDonald, C., Finn, T. & Ranjan, D. 2014b Experimental investigation of the inclined interface Richtmyer–Meshkov instability before and after reshock. Exp. Fluids 55 (1), 1–14.10.1007/s00348-013-1640-1Google Scholar
McFarland, J. A., Greenough, J. A. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84 (2), 026303.Google Scholar
McFarland, J. A., Reilly, D., Black, W., Greenough, J. A. & Ranjan, D. 2015 Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer–Meshkov instability. Phys. Rev. E 92 (1), 013023.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4 (5), 101–104.10.1007/BF01015969Google Scholar
Miller, P. L. & Dimotakis, P. E. 1996 Measurements of scalar power spectra in high Schmidt number turbulent jets. J. Fluid Mech. 308, 129–146.10.1017/S0022112096001425Google Scholar
Mohaghar, M., Carter, J., Musci, B., Reilly, D., McFarland, J. & Ranjan, D. 2017 Evaluation of turbulent mixing transition in a shock-driven variable-density flow. J. Fluid Mech. 831, 779–825.10.1017/jfm.2017.664Google Scholar
Morán-López, J. T. & Schilling, O. 2013 Multicomponent Reynolds-averaged Navier–Stokes simulations of reshocked Richtmyer–Meshkov instability-induced mixing. High Energy Density Phys. 9 (1), 112–121.10.1016/j.hedp.2012.11.001Google Scholar
Morán-López, J. T. & Schilling, O. 2014 Multi-component Reynolds-averaged Navier–Stokes simulations of Richtmyer–Meshkov instability and mixing induced by reshock at different times. Shock Waves 24 (3), 325–343.10.1007/s00193-013-0483-2Google Scholar
Morgan, B. E., Schilling, O. & Hartland, T. A. 2018 Two-length-scale turbulence model for self-similar buoyancy-, shock-, and shear-driven mixing. Phys. Rev. E 97 (1), 013104.Google Scholar
Morgan, R. V., Aure, R., Stockero, J. D., Greenough, J. A., Cabot, W., Likhachev, O. A. & Jacobs, J. W. 2012 On the late-time growth of the two-dimensional Richtmyer–Meshkov instability in shock tube experiments. J. Fluid Mech. 712, 354–383.10.1017/jfm.2012.426Google Scholar
Motl, B., Oakley, J., Ranjan, D., Weber, C., Anderson, M. & Bonazza, R. 2009 Experimental validation of a Richtmyer–Meshkov scaling law over large density ratio and shock strength ranges. Phys. Fluids 21 (12), 126102.10.1063/1.3280364Google Scholar
Olson, D. H. & Jacobs, J. W. 2009 Experimental study of Rayleigh–Taylor instability with a complex initial perturbation. Phys. Fluids 21 (3), 034103.10.1063/1.3085811Google Scholar
Orlicz, G. C., Balakumar, B. J., Tomkins, C. D. & Prestridge, K. P. 2009 A Mach number study of the Richtmyer–Meshkov instability in a varicose, heavy-gas curtain. Phys. Fluids 21 (6), 064102.10.1063/1.3147929Google Scholar
Orlicz, G. C., Balasubramanian, S. & Prestridge, K. P. 2013 Incident shock Mach number effects on Richtmyer–Meshkov mixing in a heavy gas layer. Phys. Fluids 25 (11), 114101.10.1063/1.4827435Google Scholar
Orlicz, G. C., Balasubramanian, S., Vorobieff, P. & Prestridge, K. P. 2015 Mixing transition in a shocked variable-density flow. Phys. Fluids 27 (11), 114102.10.1063/1.4935183Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.10.1017/CBO9780511840531Google Scholar
Ramaprabhu, P. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.10.1017/S0022112003007419Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.10.1146/annurev-fluid-122109-160744Google Scholar
Reese, D. T., Ames, A. M., Noble, C. D., Oakley, J. G., Rothamer, D. A. & Bonazza, R. 2018 Simultaneous direct measurements of concentration and velocity in the Richtmyer–Meshkov instability. J. Fluid Mech. 849, 541–575.10.1017/jfm.2018.419Google Scholar
Reilly, D., McFarland, J., Mohaghar, M. & Ranjan, D. 2015 The effects of initial conditions and circulation deposition on the inclined-interface reshocked Richtmyer–Meshkov instability. Exp. Fluids 56 (8), 1–16.10.1007/s00348-015-2035-2Google Scholar
Reisenhofer, R., Kiefer, J. & King, E. J. 2016 Shearlet-based detection of flame fronts. Exp. Fluids 57 (3), 41.10.1007/s00348-016-2128-6Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13 (2), 297–319.10.1002/cpa.3160130207Google Scholar
Robey, H. F., Zhou, Y., Buckingham, A. C., Keiter, P., Remington, B. A. & Drake, R. P. 2003 The time scale for the transition to turbulence in a high Reynolds number, accelerated flow. Phys. Plasmas 10 (3), 614–622.10.1063/1.1534584Google Scholar
Schilling, O. & Latini, M. 2010 High-order WENO simulations of three-dimensional reshocked Richtmyer–Meshkov instability to late times: dynamics, dependence on initial conditions, and comparisons to experimental data. Acta Math. Sci. 30 (2), 595–620.10.1016/S0252-9602(10)60064-1Google Scholar
Schilling, O., Latini, M. & Don, W. S. 2007 Physics of reshock and mixing in single-mode Richtmyer–Meshkov instability. Phys. Rev. E 76 (2), 026319.Google Scholar
Schwarzkopf, J. D., Livescu, D., Baltzer, J. R., Gore, R. A. & Ristorcelli, J. R. 2016 A two-length scale turbulence model for single-phase multi-fluid mixing. Flow Turbul. Combust. 96 (1), 1–43.10.1007/s10494-015-9643-zGoogle Scholar
Shankar, S. K. & Lele, S. K. 2014 Numerical investigation of turbulence in reshocked Richtmyer–Meshkov unstable curtain of dense gas. Shock Waves 24 (1), 79–95.10.1007/s00193-013-0478-zGoogle Scholar
Slabaugh, C. D., Pratt, A. C. & Lucht, R. P. 2015 Simultaneous 5 kHz OH-PLIF/PIV for the study of turbulent combustion at engine conditions. Appl. Phys. B 118 (1), 109–130.10.1007/s00340-014-5960-5Google Scholar
Sweeney, M. & Hochgreb, S. 2009 Autonomous extraction of optimal flame fronts in OH planar laser-induced fluorescence images. Appl. Opt. 48 (19), 3866–3877.10.1364/AO.48.003866Google Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Growth of a Richtmyer–Meshkov turbulent layer after reshock. Phys. Fluids 23 (9), 095107.10.1063/1.3638616Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2012 Physics of the single-shocked and reshocked Richtmyer–Meshkov instability. J. Turbul. 13 (1), N10.10.1080/14685248.2012.658916Google Scholar
Tomkins, C. D., Balakumar, B. J., Orlicz, G., Prestridge, K. P. & Ristorcelli, J. R. 2013 Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence. J. Fluid Mech. 735, 288–306.10.1017/jfm.2013.430Google Scholar
Tritschler, V. K., Olson, B. J., Lele, S. K., Hickel, S., Hu, X. Y. & Adams, N. A. 2014 On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface. J. Fluid Mech. 755, 429–462.10.1017/jfm.2014.436Google Scholar
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an air/SF6 interface. Shock Waves 4 (5), 247–252.10.1007/BF01416035Google Scholar
Vorobieff, P., Mohamed, N. G., Tomkins, C., Goodenough, C., Marr-Lyon, M. & Benjamin, R. F. 2003 Scaling evolution in shock-induced transition to turbulence. Phys. Rev. E 68 (6), 065301.Google Scholar
Vorobieff, P., Rightley, P. M. & Benjamin, R. F. 1998 Power-law spectra of incipient gas-curtain turbulence. Phys. Rev. Lett. 81 (11), 2240.Google Scholar
Weber, C. R., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability. Phys. Fluids 24 (7), 074105.10.1063/1.4733447Google Scholar
Weber, C. R., Haehn, N. S., Oakley, J. G., Rothamer, D. A. & Bonazza, R. 2014 An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability. J. Fluid Mech. 748, 457–487.10.1017/jfm.2014.188Google Scholar
Zabusky, N. J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31 (1), 495–536.10.1146/annurev.fluid.31.1.495Google Scholar
Zhou, Y. 2007 Unification and extension of the similarity scaling criteria and mixing transition for studying astrophysics using high energy density laboratory experiments or numerical simulations. Phys. Plasmas 14 (8), 082701.10.1063/1.2739439Google Scholar
Zhou, Y. 2017a Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720, 1–136.Google Scholar
Zhou, Y. 2017b Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 723, 1–160.Google Scholar
Zhou, Y., Cabot, W. H. & Thornber, B. 2016 Asymptotic behavior of the mixed mass in Rayleigh–Taylor and Richtmyer–Meshkov instability induced flows. Phys. Plasmas 23 (5), 052712.10.1063/1.4951018Google Scholar
Zhou, Y., Robey, H. F. & Buckingham, A. C. 2003 Onset of turbulence in accelerated high-Reynolds-number flow. Phys. Rev. E 67 (5), 056305.Google Scholar