Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-21T13:20:01.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Streamwise and doubly-localised periodic orbits in plane Poiseuille flow

Published online by Cambridge University Press:  25 November 2014

Stefan Zammert  and
Bruno Eckhardt
Stefan Zammert*
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany
Bruno Eckhardt
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany J. M. Burgerscentrum, Delft University of Technology, Mekelweg 2, 2628 CD Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study localised exact coherent structures in plane Poiseuille flow that are relative periodic orbits. They are obtained from extended states in smaller periodically continued domains, by increasing the length to obtain streamwise localisation and then by increasing the width to achieve spanwise localisation. The states maintain the travelling wave structure of the extended states, which is then modulated by a localised envelope on larger scales. In the streamwise direction, the envelope shows exponential localisation, with different exponents on the upstream and downstream sides. 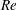The upstream exponent increases linearly with Reynolds number $\mathit{Re}$, but the downstream exponent is essentially independent of 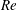$\mathit{Re}$. In the spanwise direction the decay is compatible with a power-law localisation. As the width increases the localised state undergoes further bifurcations which add additional unstable directions, so that the edge state, the relative attractor on the boundary between the laminar and turbulent motions, in the system becomes chaotic.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Waves/Free-surface Flows: Channel flow Turbulent Flows: Turbulent transition
Type
Papers
Information
Journal of Fluid Mechanics , Volume 761 , 25 December 2014 , pp. 348 - 359
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localised solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.Google Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.CrossRefGoogle ScholarPubMed
Barkley, D. & Tuckerman, L. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94, 014502.CrossRefGoogle ScholarPubMed
Brand, E. & Gibson, J. F. 2014 A doubly-localised equilibrium solution of plane Couette flow. J. Fluid Mech. 750, R1.CrossRefGoogle Scholar
Carlson, D. R., Widnall, S. E. & Peeters, M. F. 1982 A flow-visualization study of transition in plane Poiseuille flow. J. Fluid Mech. 121, 487–505.CrossRefGoogle Scholar
Chantry, M., Willis, A. P. & Kerswell, R. R. 2013 The genesis of streamwise-localised solutions from globally periodic travelling waves in pipe flow. Phys. Rev. Lett. 112, 164501.Google Scholar
Dauchot, O. & Daviaud, F. 1995 Finite amplitude perturbation and spots growth mechanism in plane Couette flow. Phys. Fluids 7, 335.CrossRefGoogle Scholar
Dijkstra, H., Wubs, F. W., Cliffe, A. K., Doedel, E., Dragomirescu, I. F., Eckhardt, B., Gelfgat, A. Yu., Hazel, A. L., Lucarini, V., Salinger, A. G., Phipps, E. T., Sanchez-Umbria, J., Schuttelaars, H., Tuckerman, L. S. & Thiele, U. 2014 Numerical bifurcation methods and their applicaton to fluid dynamics: analysis beyond simulation. Commun. Comput. Phys. 15, 1–45.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2009 Localised edge states in plane Couette flow. Phys. Fluids 21, 111701.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 228, 119–129.Google Scholar
Ehrenstein, U. & Koch, W. 1991 Three-dimensional wavelike equilibrium states in plane Poiseuille flow. J. Fluid Mech. 121, 111–148.Google Scholar
Gibson, J. F.2012 Channelflow: a spectral Navier–Stokes simulator in C $++$ . Tech. Rep., University of New Hampshire.Google Scholar
Gibson, J. F. & Brand, E. 2014 Spanwise-localised solutions of planar shear flows. J. Fluid Mech. 745, 25–61.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.CrossRefGoogle Scholar
Guennebaud, G. & Jacob, B. et al. 2010 Eigen v3, http://eigen.tuxfamily.org.Google Scholar
Hegseth, J. 1996 Turbulent spots in plane Couette flow. Phys. Rev. E 54, 4915–4923.Google Scholar
Henningson, D., Spalart, P. & Kim, J. 1987 Numerical simulations of turbulent spots in plane Poiseuille and boundary-layer flow. Phys. Fluids 30, 2914.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Khapko, T., Duguet, Y., Kreilos, T., Schlatter, P., Eckhardt, B. & Henningson, D. S. 2014 Complexity of localised coherent structures in a boundary-layer flow. Eur. Phys. J. E 37, 32.CrossRefGoogle Scholar
Khapko, T., Kreilos, T., Schlatter, P., Duguet, Y., Eckhardt, B. & Henningson, D. S. 2013 Localised edge states in the asymptotic suction boundary layer. J. Fluid Mech. 717, R6.Google Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbits near onset of chaos in plane Couette flow. Chaos 22, 047505.CrossRefGoogle ScholarPubMed
Kreilos, T., Veble, G., Schneider, T. M. & Eckhardt, B. 2013 Edge states for the turbulence transition in the asymptotic suction boundary layer. J. Fluid Mech. 726, 100–122.CrossRefGoogle Scholar
Kuznetsov, Y. A. 1998 Elements of Applied Bifurcation Theory. Springer.Google Scholar
Lagha, M. & Manneville, P. 2007 Modeling of plane Couette flow. I. Large scale flow around turbulent spots. Phys. Fluids 19, 094105.Google Scholar
Lemoult, G., Aider, J.-L. & Wesfreid, J. E. 2013 Turbulent spots in a channel: large-scale flow and self-sustainability. J. Fluid Mech. 731, R1.Google Scholar
Lemoult, G., Gumowski, K., Aider, J.-L. & Wesfreid, J. E. 2014 Turbulent spots in channel: an experimental study large-scale flow, inner structure and low order model. Eur. Phys. J. E 37, 25.CrossRefGoogle ScholarPubMed
Lundbladh, A. & Johansson, A. V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.Google Scholar
Manneville, P. 2009 Spatiotemporal perspective on the decay of turbulence in wall-bounded flows. Phys. Rev. E 79, 025301.Google ScholarPubMed
Marinc, D., Schneider, T. M. & Eckhardt, B. 2010 Localised edge states for the transition to turbulence in shear flows. In Seventh IUTAM Symp. Laminar–Turbulent Transit. (ed. Schlatter, P. & Henningson, D. S.), IUTAM Bookseries, vol. 18, pp. 253–258. Springer.Google Scholar
Mellibovsky, F., Meseguer, A., Schneider, T. & Eckhardt, B. 2009 Transition in localised pipe flow turbulence. Phys. Rev. Lett. 103, 054502.CrossRefGoogle ScholarPubMed
Melnikov, K., Kreilos, T. & Eckhardt, B. 2014 Long wavelength instability of coherent structures in plane Couette flow. Phys. Rev. E 89, 043088.Google Scholar
Moxey, D. & Barkley, D. 2010 Distinct large-scale turbulent-laminar states in transitional pipe flow. Proc. Natl Acad. Sci. USA 107, 8091–8096.CrossRefGoogle ScholarPubMed
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Nagata, M. 1997 Three-dimensional traveling-wave solutions in plane Couette flow. Phys. Rev. E 55, 2023–2025.Google Scholar
Nagata, M. & Deguchi, K. 2013 Mirror-symmetric exact coherent states in plane Poiseuille flow. J. Fluid Mech. 735, R4.CrossRefGoogle Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.CrossRefGoogle Scholar
Price, T., Brachet, M. & Pomeau, Y. 1993 Numerical characterization of localised solutions in plane Poiseuille flow. Phys. Fluids A 5, 762.Google Scholar
Schmiegel, A.1999 Transition to turbulence in linearly stable shear flows. PhD thesis, Marburg.Google Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010a Snakes and ladders: localised solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.CrossRefGoogle ScholarPubMed
Schneider, T. M., Gibson, J. F., Lagha, M., De Lillo, F. & Eckhardt, B. 2008 Laminar–turbulent boundary in plane Couette flow. Phys. Rev. E 78, 037301.CrossRefGoogle ScholarPubMed
Schneider, T. M., Marinc, D. & Eckhardt, B. 2010b Localised edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.CrossRefGoogle Scholar
Schumacher, J. & Eckhardt, B. 2001 Evolution of turbulent spots in a parallel shear flow. Phys. Rev. E 63, 046307.Google Scholar
Skufca, J., Yorke, J. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Toh, S. & Itano, T. 2003 A periodic-like solution in channel flow. J. Fluid Mech. 481, 67–76.Google Scholar
Tuckerman, L., Kreilos, T., Schrobsdorff, H., Schneider, T. M. & Gibson, J. F.2014 Turbulent-laminar patterns in plane Poiseuille flow. arXiv:1312.6783.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517.Google Scholar
Wang, J., Gibson, J. F. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98, 204501.Google Scholar
Zammert, S. & Eckhardt, B. 2014a Periodically bursting edge states in plane Poiseuille flow. Fluid Dyn. Res. 46, 041419.Google Scholar
Zammert, S. & Eckhardt, B. 2014b A spotlike edge state in plane Poiseuille flow. Proc. Appl. Maths Mech. (submitted).Google Scholar