Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T17:34:44.866Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale dynamics of dense gas compressible homogeneous isotropic turbulence

Published online by Cambridge University Press:  21 July 2017

L. Sciacovelli ,
P. Cinnella Open the ORCID record for P. Cinnella [Opens in a new window]  and
F. Grasso
L. Sciacovelli*
Affiliation:
Laboratoire DynFluid, Arts et Métiers ParisTech, 75013 Paris, France Dipartimento di Meccanica, Matematica e Management, Politenico di Bari, 70125 Bari, Italy
P. Cinnella*
Affiliation:
Laboratoire DynFluid, Arts et Métiers ParisTech, 75013 Paris, France
F. Grasso*
Affiliation:
Laboratoire DynFluid, Conservatoire National des Arts et Métiers, 75003 Paris, France
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present paper investigates the influence of dense gases governed by complex equations of state on the dynamics of homogeneous isotropic turbulence. In particular, we investigate how differences due to the complex thermodynamic behaviour and transport properties affect the small-scale structures, viscous dissipation and enstrophy generation. To this end, we carry out direct numerical simulations of the compressible Navier–Stokes equations supplemented by advanced dense gas constitutive models. The dense gas considered in the study is a heavy fluorocarbon (PP11) that is shown to exhibit an inversion zone (i.e. a region where the fundamental derivative of gas dynamics 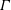$\unicode[STIX]{x1D6E4}$ is negative) in its vapour phase, for pressures and temperatures of the order of magnitude of the critical ones. Simulations are carried out at various initial turbulent Mach numbers and for two different initial thermodynamic states, one immediately outside and the other inside the inversion zone. After investigating the influence of dense gas effects on the time evolution of mean turbulence properties, we focus on the statistical properties of turbulent structures. For that purpose we carry out an analysis in the plane of the second and third invariant of the deviatoric strain-rate tensor. The analysis shows a weakening of compressive structures and an enhancement of expanding ones. Strong expansion regions are found to be mostly populated by non-focal convergence structures typical of strong compression regions, in contrast with the perfect gas that is dominated by eddy-like structures. Additionally, the contribution of non-focal expanding structures to the dilatational dissipation is comparable to that of compressed structures. This is due to the occurrence of steep expansion fronts and possibly of expansion shocklets which contribute to enstrophy generation in strong expansion regions and that counterbalance enstrophy destruction by means of the eddy-like structures.

JFM classification

Turbulent Flows: Compressible turbulence Compressible Flows: Gas dynamics Turbulent Flows: Isotropic turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 515 - 549
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, W. K. 1991 Numerical study on using sulfur hexafluoride as a wind tunnel test gas. AIAA J. 29 (12), 2179–2180.Google Scholar
Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.CrossRefGoogle Scholar
Aubard, G., Gloerfelt, X. & Robinet, J. C. 2013 Large-eddy simulation of broadband unsteadiness in a shock/boundary-layer interaction. AIAA J. 51 (10), 2395–2409.Google Scholar
Bethe, H. A.1942 The theory of shock waves for an arbitrary equation of state. Tech. Rep. 545, Office of Scientific Research and Development.Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.Google Scholar
Blaisdell, G. A., Mansour, N. N. & Reynolds, W. C. 1993 Compressibility effects on the growth and structure of homogeneous turbulent shear flow. J. Fluid Mech. 256, 443–485.Google Scholar
Bogey, C. & Bailly, C. 2004 A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 194 (1), 194–214.CrossRefGoogle Scholar
Bogey, C. & Bailly, C. 2009 Turbulence and energy budget in a self-preserving round jet: direct evaluation using large eddy simulation. J. Fluid Mech. 627, 129–160.Google Scholar
Bogey, C., De Cacqueray, N. & Bailly, C. 2009 A shock-capturing methodology based on adaptative spatial filtering for high-order non-linear computations. J. Comput. Phys. 228 (5), 1447–1465.Google Scholar
Bogey, C., Marsden, O. & Bailly, C. 2012 Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 105. J. Fluid Mech. 701, 352–385.Google Scholar
Brown, B. P. & Argrow, B. M. 2000 Application of Bethe–Zel’dovich–Thompson fluids in organic Rankine cycle engines. J. Propul. Power 16 (6), 1118–1124.CrossRefGoogle Scholar
Cantwell, B. J. 1993 On the behavior of velocity gradient tensor invariants in direct numerical simulations of turbulence. Phys. Fluids A 5 (8), 2008–2013.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Chung, T. H., Ajlan, M., Lee, L. L. & Starling, K. E. 1988 Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Engng Chem. Res. 27 (4), 671–679.Google Scholar
Chung, T. H., Lee, L. L. & Starling, K. E. 1984 Applications of kinetic gas theories and multiparameter correlation for prediction of dilute gas viscosity and thermal conductivity. Ind. Engng Chem. Fundam. 23 (1), 8–13.Google Scholar
Cinnella, P. & Congedo, P. M. 2007 Inviscid and viscous aerodynamics of dense gases. J. Fluid Mech. 580, 179–217.CrossRefGoogle Scholar
Cramer, M. S. 1989a Negative nonlinearity in selected fluorocarbons. Phys. Fluids A 1, 1894–1897.Google Scholar
Cramer, M. S. 1989b Shock splitting in single-phase gases. J. Fluid Mech. 199, 281–296.Google Scholar
Cramer, M. S. 1991 Nonclassical dynamics of classical gases. In Nonlinear Waves in Real Fluids, pp. 91–145. Springer.Google Scholar
Cramer, M. S. 2012 Numerical estimates for the bulk viscosity of ideal gases. Phys. Fluids 24, 066102.Google Scholar
Cramer, M. S. & Kluwick, A. 1984 On the propagation of waves exhibiting both positive and negative nonlinearity. J. Fluid Mech. 142, 9–37.Google Scholar
Cramer, M. S. & Tarkenton, G. M. 1992 Transonic flows of Bethe–Zel’dovich–Thompson fluids. J. Fluid Mech. 240, 197–228.Google Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 152 (2), 517–549.CrossRefGoogle Scholar
Erlebacher, G. & Sarkar, S. 1993 Statistical analysis of the rate of strain tensor in compressible homogeneous turbulence. Phys. Fluids A 5 (12), 3240–3254.Google Scholar
Gloerfelt, X. & Berland, J. 2013 Turbulent boundary-layer noise: direct radiation at Mach number 0.5. J. Fluid Mech. 723, 318–351.Google Scholar
Guardone, A. & Argrow, B. M. 2005 Nonclassical gasdynamic region of selected fluorocarbons. Phys. Fluids 17 (11), 116102.Google Scholar
Harinck, J., Turunen-Saaresti, T., Colonna, P., Rebay, S. & van Buijtenen, J. 2010 Computational study of a high-expansion ratio radial organic Rankine cycle turbine stator. Trans. ASME J. Gas Turbines Power 132 (5), 054501.Google Scholar
Horen, J., Talonpoika, T., Larjola, J. & Siikonen, T. 2002 Numerical simulation of real-gas flow in a supersonic turbine nozzle ring. Trans. ASME J. Engng Gas Turbines Power 124 (2), 395–403.Google Scholar
Jagannathan, S. & Donzis, D. A. 2016 Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J. Fluid Mech. 789, 669–707.Google Scholar
Kevlahan, N., Mahesh, K. & Lee, S. 1992 Evolution of the shock front and turbulence structures in the shock/turbulence interaction. In Studying Turbulence Using Numerical Simulation Databases, vol. 1, pp. 277–292. Center for Turbulence Research.Google Scholar
Kida, S. & Orszag, S. A. 1989 Enstrophy budget in decaying compressible turbulence. J. Sci. Comput. 5, 1–34.Google Scholar
Kirillov, N. 2004 Analysis of modern natural gas liquefaction technologies. Chem. Petrol. Engng 40 (7–8), 401–406.Google Scholar
Kovasznay, L. S. G. 1953 Turbulence in supersonic flow. J. Aeronaut. Soc. 20, 657–682.Google Scholar
Lee, K., Girimaji, S. S. & Kerimo, J. 2009 Effect of compressibility on turbulent velocity gradients and small-scale structure. J. Turbul. 10, N9.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1991 Eddy shocklets in decaying compressible turbulence. Phys. Fluids A 3, 657–664.Google Scholar
Lemmon, E. W. & Span, R. 2006 Short fundamental equations of state for 20 industrial fluids. J. Chem. Engng Data 51 (3), 785–850.CrossRefGoogle Scholar
Lesieur, M 2008 Turbulence in Fluids, Fluid Mechanics and its Applications. Springer.Google Scholar
Martín, J., Ooi, A., Chong, M. S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336–2346.Google Scholar
Martin, J. J. & Hou, Y. C. 1955 Development of an equation of state for gases. AIChE J. 1 (2), 142–151.Google Scholar
Monaco, J. F., Cramer, M. S. & Watson, L. T. 1997 Supersonic flows of dense gases in cascade configurations. J. Fluid Mech. 330, 31–59.CrossRefGoogle Scholar
Ooi, A., Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Passot, T. & Pouquet, A. 1987 Numerical simulation of compressible homogeneous flows in the turbulent regime. J. Fluid Mech. 181, 441–466.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19 (1), 125–155.Google Scholar
Pirozzoli, S. & Grasso, F. 2004 Direct numerical simulations of isotropic compressible turbulence: influence of compressibility on dynamics and structures. Phys. Fluids 16 (12), 4386–4407.Google Scholar
Poling, B. E., Prausnitz, J. M., O’Connell, J. P. & Reid, R. C. 2001 The Properties of Gases and Liquids, vol. 5. McGraw-Hill.Google Scholar
Ristorcelli, J. R. & Blaisdell, G. A. 1997 Consistent initial conditions for the DNS of compressible turbulence. Phys. Fluids 9 (1), 4–6.Google Scholar
Rusak, Z. & Wang, C. 1997 Transonic flow of dense gases around an airfoil with a parabolic nose. J. Fluid Mech. 346, 1–21.CrossRefGoogle Scholar
Samtaney, R., Pullin, D. I. & Kosovic, B. 2001 Direct numerical simulation of decaying compressible turbulence and shocklet statistics. Phys. Fluids 13 (5), 1415–1430.Google Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 227, 473–493.Google Scholar
Sciacovelli, L. & Cinnella, P. 2014 Numerical study of multistage transcritical organic Rankine cycle axial turbines. J. Gas Turbines Power 136 (2), 082604.Google Scholar
Sciacovelli, L., Cinnella, P., Content, C. & Grasso, F. 2016 Dense gas effects in inviscid homogeneous isotropic turbulence. J. Fluid Mech. 800, 140–179.Google Scholar
Soria, J. & Cantwell, B. J. 1994 Topological visualisation of focal structures in free shear flows. Appl. Sci. Res. 53 (3–4), 375–386.CrossRefGoogle Scholar
Stryjek, R. & Vera, J. H. 1986 PRSV2: a cubic equation of state for accurate vapor–liquid equilibria calculations. Canad. J. Chem. Engng 64 (5), 820–826.Google Scholar
Thompson, P. A. 1971 A fundamental derivative in gasdynamics. Phys. Fluids 14 (9), 1843–1849.Google Scholar
Thompson, P. A. & Lambrakis, K. C. 1973 Negative shock waves. J. Fluid Mech. 60 (01), 187–208.Google Scholar
Van der Waals, J. D.1873 Doctoral dissertation. PhD thesis, University of Leiden.Google Scholar
Wang, J., Shi, Y., Wang, L., Xiao, Z., He, X. T. & Chen, S. 2012 Effect of compressibility on the small-scale structures in isotropic turbulence. J. Fluid Mech. 713, 588–631.Google Scholar
Wang, L. & Peters, N. 2013 A new view of flow topology and conditional statistics in turbulence. Phil. Trans. R. Soc. Lond. A 371 (1982), 20120169.Google ScholarPubMed
Wheeler, A. P. S. & Ong, J. 2013 The role of dense gas dynamics on organic Rankine cycle turbine performance. Trans. ASME J. Engng Gas Turbines Power 135 (10), 102603.Google Scholar
Wheeler, A. P. S. & Ong, J. 2014 A study of the three-dimensional unsteady real-gas flows within a transonic ORC turbine. In Proceedings of the ASME Turbo Expo 2014, GT2014, June 16–20, 2014, Dusseldorf, Germany. ASME.Google Scholar
Zamfirescu, C. & Dincer, I. 2009 Performance investigation of high-temperature heat pumps with various BZT working fluids. Thermochim. Acta 488, 66–77.Google Scholar
Zel’Dovich, Y. B. & Raizer, Y. P. 1966 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Academic.Google Scholar