Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hu, Nan
2018.
Empirical Model of Wall Pressure Spectra in Adverse Pressure Gradients.
AIAA Journal,
Vol. 56,
Issue. 9,
p.
3491.
Erbig, Lars
Hu, Nan
and
Lardeau, Sylvain
2018.
Experimental and Numerical Study of Passive Gap Noise.
Avallone, Francesco
Casalino, Damiano
and
Ragni, Daniele
2018.
Unsteady coherent surface-pressure fluctuations from time-averaged flow data with given two-point statistics.
Hu, Nan
Appel, Christina
Haxter, Stefan
Callsen, Sören
and
Klabes, Alexander
2019.
Simulation of wall pressure fluctuations on Airbus-A320 fuselage in cruise flight condition.
Grasso, G.
Jaiswal, P.
Wu, H.
Moreau, S.
and
Roger, M.
2019.
Analytical models of the wall-pressure spectrum under a turbulent boundary layer with adverse pressure gradient.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
1007.
Klabes, Alexander
Callsen, Sören
Herr, Michaela
and
Appel, Christina
2019.
Flinovia—Flow Induced Noise and Vibration Issues and Aspects-II.
p.
309.
Erbig, Lars
and
Maihöfer, Martin
2019.
A Hybrid RANS/LES for Automotive Gap Noise Simulations.
Enghardt, Lars
2019.
Aeroacoustics research in Europe: The CEAS-ASC report on 2017 highlights.
Journal of Sound and Vibration,
Vol. 450,
Issue. ,
p.
175.
Gao, Wei
Cheng, Wan
and
Samtaney, Ravi
2020.
Large-eddy simulations of turbulent flow in a channel with streamwise periodic constrictions.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Deng, Chao
Chen, Chunjun
Sun, Qi
Wang, Dongwei
and
He, Zhiying
2020.
Interference Elimination of Wall Fluctuation Pressure Test Signal of High-Speed Train Based on Phase Space Reconstruction and Vibration Interference Model.
Fluctuation and Noise Letters,
Vol. 19,
Issue. 02,
p.
2050020.
Camussi, Roberto
and
Bennett, Gareth J.
2020.
Aeroacoustics research in Europe: The CEAS-ASC report on 2019 highlights.
Journal of Sound and Vibration,
Vol. 484,
Issue. ,
p.
115540.
Ananthan, V.B.
Bernicke, P.
Akkermans, R.A.D.
Hu, T.
and
Liu, P.
2020.
Effect of porous material on trailing edge sound sources of a lifting airfoil by zonal Overset-LES.
Journal of Sound and Vibration,
Vol. 480,
Issue. ,
p.
115386.
Erbig, Lars
and
Lardeau, Sylvain
2020.
Progress in Hybrid RANS-LES Modelling.
Vol. 143,
Issue. ,
p.
73.
Hu, Nan
Appel, Christina
Haxter, Stefan
Callsen, Sören
and
Klabes, Alexander
2021.
Simulation of Surface Pressure Fluctuations on an Airbus-A320 Fuselage at Cruise Conditions.
AIAA Journal,
Vol. 59,
Issue. 5,
p.
1585.
Hu, Nan
2021.
Coherence of wall pressure fluctuations in zero and adverse pressure gradients.
Journal of Sound and Vibration,
Vol. 511,
Issue. ,
p.
116316.
Li, Yuhui
Miao, Xuhong
Jia, Di
Wang, Xueren
and
Li, Lei
2021.
Research on prediction method of pulsating pressure of underwater vehicles.
Ocean Engineering,
Vol. 219,
Issue. ,
p.
108267.
Robin, Olivier
Pachebat, Marc
Totaro, Nicolas
and
Berry, Alain
2021.
Flinovia—Flow Induced Noise and Vibration Issues and Aspects-III.
p.
87.
Hillcoat, Sophie
and
Hickey, Jean-Pierre
2021.
Pressure fluctuations under a turbulent boundary layer with transpiration cooling.
Muthu, Satish
Bhushan, Shanti
and
Keith Walters, D.
2021.
Identification of a Pressure–Strain Correlation-Based Bypass Transition Onset Marker.
Journal of Fluids Engineering,
Vol. 143,
Issue. 10,
Teruna, Christopher
Avallone, Francesco
Ragni, Daniele
and
Casalino, Damiano
2021.
On the noise reduction of a porous trailing edge applied to an airfoil at lifting condition.
Physics of Fluids,
Vol. 33,
Issue. 5,
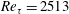 $\mathit{Re}_{\unicode[STIX]{x1D70F}}=2513$ and
$\mathit{Re}_{\unicode[STIX]{x1D70F}}=2513$ and 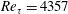 $\mathit{Re}_{\unicode[STIX]{x1D70F}}=4357$. To determine fluctuating pressure, a Poisson equation is solved with an unsteady right-hand side source term derived from the synthetic turbulence realisation. The Poisson equation is solved via fast Fourier transform using Hockney’s method. Due to its efficiency, the applied procedure enables us to study, for high Reynolds number flow, the effect of variations of the modelled turbulence characteristics on the resulting wall pressure spectrum. The contributions to wall pressure fluctuations from the mean-shear turbulence interaction term and the turbulence–turbulence interaction term are studied separately. The results show that both contributions have the same order of magnitude. Simulated one-point spectra and two-point cross-correlations of wall pressure fluctuations are analysed in detail. Convective features of the fluctuating pressure field are well determined. Good agreement for the characteristics of the wall pressure fluctuations is found between the present results and databases from other investigators.
$\mathit{Re}_{\unicode[STIX]{x1D70F}}=4357$. To determine fluctuating pressure, a Poisson equation is solved with an unsteady right-hand side source term derived from the synthetic turbulence realisation. The Poisson equation is solved via fast Fourier transform using Hockney’s method. Due to its efficiency, the applied procedure enables us to study, for high Reynolds number flow, the effect of variations of the modelled turbulence characteristics on the resulting wall pressure spectrum. The contributions to wall pressure fluctuations from the mean-shear turbulence interaction term and the turbulence–turbulence interaction term are studied separately. The results show that both contributions have the same order of magnitude. Simulated one-point spectra and two-point cross-correlations of wall pressure fluctuations are analysed in detail. Convective features of the fluctuating pressure field are well determined. Good agreement for the characteristics of the wall pressure fluctuations is found between the present results and databases from other investigators.