Article contents
Shape design for stabilizing microparticles in inertial microfluidic flows
Published online by Cambridge University Press: 14 January 2020
Abstract
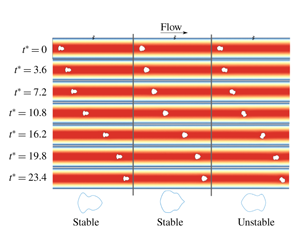
Design of isolated microparticles which stabilize at the centreline of a channel flow is examined numerically, for moderate Reynolds numbers ( $10\leqslant Re\leqslant 80$). This problem is motivated by the need for the design of shaped particle carriers for use in next generation microfluidic cell analysis devices. Stability metrics for particles with arbitrary shapes are formulated based on linear stability theory. Particle shape is parametrized by a compact, non-uniform rational B-spline-based representation. Shape design is posed as an optimization problem and solved using adaptive Bayesian optimization. We focus on designing particles for stability at the channel centreline robust to perturbations. Our results indicate that centreline focusing particles are families of characteristic ‘fish’/‘bottle’/‘dumbbell’-like shapes, exhibiting fore–aft asymmetry. A parametric exploration is then performed to identify stable particle designs at different
$10\leqslant Re\leqslant 80$). This problem is motivated by the need for the design of shaped particle carriers for use in next generation microfluidic cell analysis devices. Stability metrics for particles with arbitrary shapes are formulated based on linear stability theory. Particle shape is parametrized by a compact, non-uniform rational B-spline-based representation. Shape design is posed as an optimization problem and solved using adaptive Bayesian optimization. We focus on designing particles for stability at the channel centreline robust to perturbations. Our results indicate that centreline focusing particles are families of characteristic ‘fish’/‘bottle’/‘dumbbell’-like shapes, exhibiting fore–aft asymmetry. A parametric exploration is then performed to identify stable particle designs at different  $k$ values (particle chord-to-channel width ratio) and
$k$ values (particle chord-to-channel width ratio) and  $Re$ values (
$Re$ values ( $0.1\leqslant k\leqslant 0.4,10\leqslant Re\leqslant 80$). Particles at high
$0.1\leqslant k\leqslant 0.4,10\leqslant Re\leqslant 80$). Particles at high  $k$ values and
$k$ values and  $Re$ values are highly stabilized when compared to those at low
$Re$ values are highly stabilized when compared to those at low  $k$ values and
$k$ values and  $Re$ values. We validate the performance of designed particles to perturbations in flow using detailed fluid–structure interaction simulations over different
$Re$ values. We validate the performance of designed particles to perturbations in flow using detailed fluid–structure interaction simulations over different  $k$ values and
$k$ values and  $Re$ values. We identify a basin of attraction around the centreline, within which any arbitrary release results in rotationally stable centreline focusing. We find that this basin spans larger release angle ranges and lateral locations (tending to the channel width) for narrower channels. This effectively standardizes the notion of global focusing using the current stability paradigm in narrow channels, which eliminates the need for an independent design for global focusing in such configurations. The framework detailed in this work is illustrated for two-dimensional cases and is generalizable to stability in three-dimensional flow fields. The current formulation is agnostic to
$Re$ values. We identify a basin of attraction around the centreline, within which any arbitrary release results in rotationally stable centreline focusing. We find that this basin spans larger release angle ranges and lateral locations (tending to the channel width) for narrower channels. This effectively standardizes the notion of global focusing using the current stability paradigm in narrow channels, which eliminates the need for an independent design for global focusing in such configurations. The framework detailed in this work is illustrated for two-dimensional cases and is generalizable to stability in three-dimensional flow fields. The current formulation is agnostic to  $Re$ and particle/channel geometry, which indicates substantial potential for integration with imaging flow cytometry tools and microfluidic biosensing assays.
$Re$ and particle/channel geometry, which indicates substantial potential for integration with imaging flow cytometry tools and microfluidic biosensing assays.
- Type
- JFM Papers
- Information
- Copyright
- © 2020 Cambridge University Press
References
Kommajosula et al. supplementary movie 1
Long channel FSI simulation for highly stable particle at Re = 20, k = 0.3 (angular perturbation)
Kommajosula et al. supplementary movie 2
Long channel FSI simulation for weakly stable particle at Re = 20, k = 0.3 (angular perturbation)
Kommajosula et al. supplementary movie 3
Long channel FSI simulation for unstable particle at Re = 20, k = 0.3 (angular perturbation)
Kommajosula et al. supplementary movie 4
Long channel FSI simulation for stable particle at Re = 20, k = 0.4 (angular perturbation)
Kommajosula et al. supplementary movie 5
Long channel FSI simulation for unstable particle at Re = 20, k = 0.4 (angular perturbation)
Kommajosula et al. supplementary movie 6
Long channel FSI simulation for stable particle at Re = 80, k = 0.4 (angular perturbation)
Kommajosula et al. supplementary movie 7
Long channel FSI simulation for unstable particle at Re = 80, k = 0.4 (angular perturbation)
Kommajosula et al. supplementary movie 8
Long channel FSI simulation for stable particle-1 at Re = 20, k = 0.7 (lateral perturbation)
- 4
- Cited by


