Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-01T01:07:55.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Radiation of short waves from the resonantly excited capillary–gravity waves

Published online by Cambridge University Press:  24 November 2016

M. Hirata ,
S. Okino  and
H. Hanazaki
M. Hirata
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto-daigaku Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
S. Okino
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto-daigaku Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
H. Hanazaki*
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto-daigaku Katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Capillary–gravity waves resonantly excited by an obstacle (Froude number: 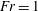$Fr=1$) are investigated by the numerical solution of the Euler equations. The radiation of short waves from the long nonlinear waves is observed when the capillary effects are weak (Bond number: 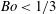$Bo<1/3$). The upstream-advancing solitary wave radiates a short linear wave whose phase velocity is equal to the solitary waves and group velocity is faster than the solitary wave (soliton radiation). Therefore, the short wave is observed upstream of the foremost solitary wave. The downstream cnoidal wave also radiates a short wave which propagates upstream in the depression region between the obstacle and the cnoidal wave. The short wave interacts with the long wave above the obstacle, and generates a second short wave which propagates downstream. These generation processes will be repeated, and the number of wavenumber components in the depression region increases with time to generate a complicated wave pattern. The upstream soliton radiation can be predicted qualitatively by the fifth-order forced Korteweg–de Vries equation, but the equation overestimates the wavelength since it is based on a long-wave approximation. At a large Bond number of 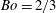$Bo=2/3$, the wave pattern has the rotation symmetry against the pattern at 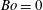$Bo=0$, and the depression solitary waves propagate downstream.

JFM classification

Waves/Free-surface Flows: Capillary waves Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , pp. 5 - 24
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akylas, T. R. 1984 On the excitation of long nonlinear water waves by a moving pressure distribution. J. Fluid Mech. 141, 455–466.Google Scholar
Casciola, C. M. & Landrini, M. 1996 Nonlinear long waves generated by a moving pressure disturbance. J. Fluid Mech. 325, 399–418.CrossRefGoogle Scholar
Champneys, R. A., Vanden-Broeck, J. -M. & Lord, J. G. 2002 Do true elevation gravity-capillary solitary waves exist? A numerical investigation. J. Fluid Mech. 454, 403–417.CrossRefGoogle Scholar
Conforti, M., Baronio, F. & Trillo, S. 2014 Resonant radiation shed by dispersive shock waves. Phys. Rev. A 89, 013807.CrossRefGoogle Scholar
Efimov, A., Yulin, A. V., Skryabin, D. V., Knight, J. C., Joly, N., Omenetto, F. G., Taylor, A. J. & Russell, P. 2005 Interaction of an optical soliton with a dispersive wave. Phys. Rev. Lett. 95, 213902.Google Scholar
Falcon, E., Laroche, C. & Fauve, S. 2002 Observation of depression solitary surface waves on a thin fluid layer. Phys. Rev. Lett. 89, 204501.CrossRefGoogle ScholarPubMed
Grimshaw, R. 1990 Resonant flow of rotating fluid past an obstacle: the general case. Stud. Appl. Maths. 83, 249–269.Google Scholar
Grimshaw, R. H. J. & Smyth, N. 1986 Resonant flow of a stratified fluid over topography. J. Fluid Mech. 169, 429–464.Google Scholar
Hanazaki, H. 1992 A numerical study of nonlinear waves in a transcritical flow of stratified fluid past an obstacle. Phys. Fluids A 4, 2230–2243.CrossRefGoogle Scholar
Hanazaki, H. 1993 Upstream-advancing nonlinear waves excited in an axisymmetric transcritical flow of rotating fluid. Phys. Fluids A 5, 1201–1205.CrossRefGoogle Scholar
Hanazaki, H. 2003 Recirculation eddies generated by solitary waves in a rotating fluid. J. Phys. Soc. Japan 72, 516–525.CrossRefGoogle Scholar
Harlow, F. H. & Welch, J. E. 1965 Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface. Phys. Fluids 8, 2182–2189.Google Scholar
Hunter, J. K. & Vanden-Broeck, J. -M. 1983 Solitary and periodic gravity-capillary waves of finite amplitude. J. Fluid Mech. 134, 205–219.Google Scholar
Karpman, V. I. 1993 Radiation by solitons due to higher-order dispersion. Phys. Rev. E 47, 2073–2082.Google Scholar
Karpman, V. I. 1998 Radiation by weakly nonlinear shallow-water solitons due to higher-order dispersion. Phys. Rev. E 58, 5070–5080.Google Scholar
Kawahara, T. 1972 Oscillatory solitary waves in dispersive media. J. Phys. Soc. Japan 33, 260–264.Google Scholar
Kawamura, T., Takami, H. & Kuwahara, K. 1986 Computation of high Reynolds number flow around a circular cylinder with surface roughness. Fluid Dyn. Res. 1, 145–162.Google Scholar
Korteweg, D. J. & de Vries, G. 1895 On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. 39, 422–443.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Lee, S. -J., Yates, G. T. & Wu, T. Y. 1989 Experiments and analyses of upstream-advancing solitary waves generated by moving disturbances. J. Fluid Mech. 199, 569–593.CrossRefGoogle Scholar
Leibovich, S. 1970 Weakly nonlinear waves in rotating fluids. J. Fluid Mech. 42, 803–822.Google Scholar
Milewski, P. A. & Vanden-Broeck, J.-M. 1999 Time dependent gravity-capillary flows past an obstacle. Wave Motion 29, 63–79.CrossRefGoogle Scholar
Skryabin, D. V. & Yulin, A. V. 2005 Theory of generation of new frequencies by mixing of solitons and dispersive waves in optical fibers. Phys. Rev. E. 72, 016619.CrossRefGoogle ScholarPubMed
Thompson, J. F., Thames, F. C. & Mastin, C. W. 1974 Automatic numerical generation of body-fitted curvilinear coordinate system for field containing any number of arbitrary two-dimensional bodies. J. Comput. Phys. 15, 299–319.Google Scholar
Vanden-Broeck, J. -M. 1991 Elevation solitary waves with surface tension. Phys. Fluids A 3, 2659–2663.Google Scholar
Wu, T. Y. 1987 Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 184, 75–99.CrossRefGoogle Scholar
Yang, T. S. & Akylas, T. R. 1996 Weakly nonlocal gravity capillary solitary waves. Phys. Fluids A 8, 1506–1514.Google Scholar
Zhang, D. & Chwang, A. T. 1996 Numerical study of nonlinear shallow water waves produced by a submerged moving disturbance in viscous flow. Phys. Fluids. 8, 147–155.Google Scholar
Zhang, D. & Chwang, A. T. 1999 On solitary waves forced by underwater moving objects. J. Fluid Mech. 389, 119–135.Google Scholar
Zhu, Y. 1995 Resonant generation of nonlinear capillary gravity waves. Phys. Fluids. 7, 2294–2296.CrossRefGoogle Scholar