Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T06:57:38.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadrupolar flows around spots in internal shear flows

Published online by Cambridge University Press:  06 April 2020

Zhe Wang Open the ORCID record for Zhe Wang [Opens in a new window] ,
Claude Guet Open the ORCID record for Claude Guet [Opens in a new window] ,
Romain Monchaux Open the ORCID record for Romain Monchaux [Opens in a new window] ,
Yohann Duguet  and
Bruno Eckhardt Open the ORCID record for Bruno Eckhardt [Opens in a new window]
Zhe Wang*
Affiliation:
Energy Research Institute at Nanyang Technological University (ERI@N), Nanyang Technological University, 639798Singapore Interdisciplinary Graduate School, Nanyang Technological University, 639798Singapore School of Materials Science and Engineering, Nanyang Technological University, 639798Singapore
Claude Guet
Affiliation:
Energy Research Institute at Nanyang Technological University (ERI@N), Nanyang Technological University, 639798Singapore School of Materials Science and Engineering, Nanyang Technological University, 639798Singapore
Romain Monchaux
Affiliation:
IMSIA, ENSTA-ParisTech/CNRS/CEA/EDF, Institut Polytechnique de Paris, 91762Palaiseau, France
Yohann Duguet
Affiliation:
LIMSI-CNRS, Université Paris Saclay, 91403Orsay, France
Bruno Eckhardt
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, 35032Marburg, Germany
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

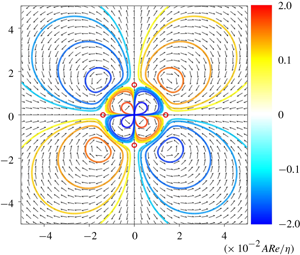
Turbulent spots occur in shear flows confined between two walls and are surrounded by robust quadrupolar flows. Although the far-field decay of such large-scale flows has been reported to be exponential, we predict a different algebraic decay for the case of plane Couette flow. We address this problem theoretically, by modelling an isolated spot as an obstacle in a linear plane shear flow with free-slip boundary conditions at the walls. By seeking invariant solutions in a co-moving Lagrangian frame and using geometric scale separation, a set of differential equations governing large-scale flows is derived from the Navier–Stokes equations and solved analytically. The wall-normal velocity turns out to be exponentially localised in the plane, while the quadrupolar in-plane velocity field, after wall-normal averaging, features a superposition of algebraic and exponential decays. The algebraic decay exponent is $-3$. The quadrupolar angular dependence stems from (i) the shearing of the streamwise velocity and (ii) the breaking of the spanwise homogeneity. Near the spot, exponentially decaying solutions can generate reversed quadrupolar flows. Eventually, by noting that the algebraically decaying in-plane flow is two-dimensional and harmonic, we suggest a topological origin to the quadrupolar large-scale flow.

JFM classification

Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A27
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables. Courier Corporation.Google Scholar
Alavyoon, F., Henningson, D. S. & Alfredsson, P. H. 1986 Turbulent spots in plane Poiseuille flow-flow visualization. Phys. Fluids 29 (4), 1328–1331.CrossRefGoogle Scholar
Barkley, D. & Tuckerman, L. S. 2007 Mean flow of turbulent-laminar patterns in plane Couette flow. J. Fluid Mech. 576, 109–137.CrossRefGoogle Scholar
Blake, J. R. 1971 A note on the image system for a Stokeslet in a no-slip boundary. Math. Proc. Camb. Phil. Soc. 70 (2), 303–310.CrossRefGoogle Scholar
Bottin, S., Dauchot, O. & Daviaud, F. 1997 Intermittency in a locally forced plane Couette flow. Phys. Rev. Lett. 79 (22), 4377–4380.CrossRefGoogle Scholar
Bottin, S., Dauchot, O. & Daviaud, F. 1998 Experimental evidence of streamwise vortices as finite amplitude solutions in transitional plane Couette flow. Phys. Fluids 10 (10), 2597–2607.CrossRefGoogle Scholar
Brand, E. & Gibson, J. F. 2014 A doubly localized equilibrium solution of plane Couette flow. J. Fluid Mech. 750, R3.CrossRefGoogle Scholar
Carlson, D. R., Widnall, S. E. & Peeters, M. F. 1982 A flow-visualization study of transition in plane Poiseuille flow. J. Fluid Mech. 121, 487–505.CrossRefGoogle Scholar
Chaikin, P. M. & Lubensky, T. C. 1995 Principles of Condensed Matter Physics. Cambridge University Press.CrossRefGoogle Scholar
Chantry, M., Tuckerman, L. S. & Barkley, D. 2016 Turbulent-laminar patterns in shear flows without walls. J. Fluid Mech. 791, R8.CrossRefGoogle Scholar
Chantry, M., Tuckerman, L. S. & Barkley, D. 2017 Universal continuous transition to turbulence in a planar shear flow. J. Fluid Mech. 824, R1.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.CrossRefGoogle Scholar
Couliou, M. & Monchaux, R. 2015 Large-scale flows in transitional plane Couette flow: a key ingredient of the spot growth mechanism. Phys. Fluids 27 (3), 034101.CrossRefGoogle Scholar
Couliou, M. & Monchaux, R. 2016 Spreading of turbulence in plane Couette flow. Phys. Rev. E 93, 013108.Google ScholarPubMed
Couliou, M. & Monchaux, R. 2017 Growth dynamics of turbulent spots in plane Couette flow. J. Fluid Mech. 819, 1–20.CrossRefGoogle Scholar
Couliou, M. & Monchaux, R. 2018 Childhood of turbulent spots in a shear flow. Phys. Rev. F 3 (12), 123901.Google Scholar
Dauchot, O. & Daviaud, F. 1995a Finite amplitude perturbation and spots growth mechanism in plane Couette flow. Phys. Fluids 7, 335–343.CrossRefGoogle Scholar
Dauchot, O. & Daviaud, F. 1995b Streamwise vortices in plane Couette flow. Phys. Fluids 7, 901–903.CrossRefGoogle Scholar
Daviaud, F., Hegseth, J. & Bergé, P. 1992 Subcritical transition to turbulence in plane Couette flow. Phys. Rev. Lett. 69, 2511–2514.CrossRefGoogle ScholarPubMed
Duguet, Y., Maitre, O. L. & Schlatter, P. 2011 Stochastic and deterministic motion of a laminar-turbulent front in a spanwisely extended Couette flow. Phys. Rev. E 84 (6), 066315.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar-turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.CrossRefGoogle ScholarPubMed
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.CrossRefGoogle Scholar
Eckhardt, B. & Pandit, R. 2003 Noise correlations in shear flows. Eur. Phys. J. B 33 (3), 373–378.CrossRefGoogle Scholar
Emmons, H. W. 1951 The laminar-turbulent transition in a boundary layer-part I. J. Aeronaut. Sci. 18 (7), 490–498.Google Scholar
Gradshteyn, I. S. & Ryžhik, I. M. 2014 Table of Integrals, Series, and Products. Academic Press.Google Scholar
Grenier, E. & Nguyen, T. T. 2019 Green function of Orr–Sommerfeld equations away from critical layers. SIAM J. Math. Anal. 51 (2), 1279–1296.CrossRefGoogle Scholar
Guckenheimer, J. & Holmes, P. 2013 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer.Google Scholar
Henningson, D. S. & Kim, J. 1991 On turbulent spots in plane Poiseuille flow. J. Fluid Mech. 228, 183–205.Google Scholar
Howison, S. 2005 Practical Applied Mathematics: Modelling, Analysis, Approximation. Cambridge University Press.CrossRefGoogle Scholar
Ishida, T., Duguet, Y. & Tsukahara, T. 2016 Transitional structures in annular Poiseuille flow depending on radius ratio. J. Fluid Mech. 794, R2.CrossRefGoogle Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.CrossRefGoogle Scholar
Jost, J. 1995 Riemannian Geometry and Geometric Analysis. Springer.CrossRefGoogle Scholar
Kelvin, Lord 1887 On ship waves. Proc. Inst. Mech. Engrs 38, 641–649.Google Scholar
Klotz, L., Lemoult, G., Frontczak, I., Tuckerman, L. S. & Wesfreid, J. E. 2017 Couette–Poiseuille flow experiment with zero mean advection velocity: subcritical transition to turbulence. Phys. Rev. F 2, 043904.Google Scholar
Lagha, M. & Manneville, P. 2007 Modeling of plane Couette flow. I. Large scale flow around turbulent spots. Phys. Fluids 19, 094105.Google Scholar
Lefschetz, S. 1949 Introduction to Topology. Princeton University Press.CrossRefGoogle Scholar
Lemoult, G., Aider, J. L. & Wesfreid, J. E. 2013 Turbulent spots in a channel: large-scale flow and self-sustainability. J. Fluid Mech. 731, R1.CrossRefGoogle Scholar
Li, F. & Widnall, S. E. 1989 Wave patterns in plane Poiseuille flow created by concentrated disturbances. J. Fluid Mech. 208, 639–656.CrossRefGoogle Scholar
Liron, N. & Mochon, S. 1976 Stokes flow for a Stokeslet between two parallel flat plates. J. Engng Maths 10 (4), 287–303.CrossRefGoogle Scholar
Lundbladh, A. & Johansson, A. V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.CrossRefGoogle Scholar
Marqués, F. 1990 On boundary conditions for velocity potentials in confined flows: application to Couette flow. Phys. Fluids 2 (3), 729–737.CrossRefGoogle Scholar
Prigent, A., Grégoire, G., Chaté, H. & Dauchot, O. 2003 Long-wavelength modulation of turbulent shear flows. Physica D 174 (1-4), 100–113.Google Scholar
Prigent, A., Grégoire, G., Chaté, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89, 014501.CrossRefGoogle ScholarPubMed
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. A 174, 935–982.Google Scholar
Ritter, P., Zammert, S., Song, B., Eckhardt, B. & Avila, M. 2018 Analysis and modeling of localized invariant solutions in pipe flow. Phys. Rev. F 3, 013901.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Applics 7, 137–146.CrossRefGoogle Scholar
Samanta, D., Lozar, A. D. & Hof, B. 2011 Experimental investigation of laminar turbulent intermittency in pipe flow. J. Fluid Mech. 681, 193–204.CrossRefGoogle Scholar
Schumacher, J. & Eckhardt, B. 2001 Evolution of turbulent spots in a parallel shear flow. Phys. Rev. E 63, 046307.Google Scholar
Tardu, S. 2012 Forcing a low Reynolds number channel flow to generate synthetic turbulent-like structures. Comput. Fluids 55, 101–108.CrossRefGoogle Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. 164 (919), 476–490.CrossRefGoogle Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.CrossRefGoogle Scholar
Wang, Z.2019 Localised and bifurcating structures in planar shear flows. PhD thesis, Nanyang Technological University.Google Scholar