Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T18:20:53.414Z Has data issue: false hasContentIssue false
  • English
  • Français

Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces

Published online by Cambridge University Press:  22 October 2015

J. Seo ,
R. García-Mayoral  and
A. Mani
J. Seo
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA
R. García-Mayoral
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
A. Mani*
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Superhydrophobic surfaces can entrap gas pockets within their grooves when submerged in water. Such a mixed-phase boundary is shown to result in an effective slip velocity on the surface, and has promising potential for drag reduction and energy-saving in hydrodynamic applications. The target flow regime, in most such applications, is a turbulent flow. Previous analyses of this problem involved direct numerical simulations of turbulence with the superhydrophobic surface modelled as a flat boundary, but with a heterogeneous mix of slip and no-slip boundary conditions corresponding to the surface texture. Analysis of the kinematic data from these simulations has helped to establish the magnitude of drag reduction for various texture topologies. The present work is the first investigation that, alongside a kinematic investigation, addresses the robustness of superhydrophobic surfaces by studying the load fields obtain from data from direct numerical simulations (DNS). The key questions at the focus of this work are: does a superhydrophobic surface induce a different pressure field compared to a flat surface? If so, how does this difference scale with system parameters, and when does it become significant that it can deform the air–water interface and potentially rapture the entrapped gas pockets? To this end, we have performed DNS of turbulent channel flows subject to superhydrophobic surfaces over a wide range of texture sizes spanning values from 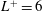$L^{+}=6$ to 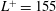$L^{+}=155$ when expressed in terms of viscous units. The pressure statistics at the wall are decomposed into two contributions: one coherent, caused by the stagnation of slipping flow hitting solid posts, and one time-dependent, caused by overlying turbulence. The results show that the larger texture size intensifies the contribution of stagnation pressure, while the contribution from turbulence is essentially insensitive to 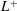$L^{+}$. The two-dimensional stagnation pressure distribution at the wall and the pressure statistics in the wall-normal direction are found to be self-similar for different 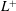$L^{+}$. The scaling of the induced pressure and the consequent deformations of the air–water interface are analysed. Based on our results, an upper bound on the texture wavelength is quantified that limits the range of robust operation of superhydrophobic surfaces when exposed to high-speed flows. Our results indicate that when the system parameters are expressed in terms of viscous units, the main parameters controlling the problem are 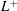$L^{+}$ and a Weber number based on inner dimensions; We obtain good collapse when all our results are expressed in wall units, independently of the Reynolds number.

JFM classification

Flow Control: Drag reduction Interfacial Flows (free surface): Interfacial Flows (free surface) Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 448 - 473
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V. & Jone, A. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.Google Scholar
Belyaev, A. V. & Vinogradova, O. I. 2010 Effective slip in pressure-driven flow past super-hydrophobic stripes. J. Fluid Mech. 652, 489–499.CrossRefGoogle Scholar
Bidkar, R. A., Leblanc, L., Kulkarni, A. J., Bahadur, V., Ceccio, S. L. & Perlin, M. 2014 Skin-friction drag reduction in the turbulent regime using random-textured hydrophobic surfaces. Phys. Fluids 26, 085108.CrossRefGoogle Scholar
Bose, S. T., Moin, P. & You, D. 2010 Grid-independent large-eddy simulation using explicit filtering. Phys. Fluids 22, 105103.CrossRefGoogle Scholar
Busse, A. & Sandham, N. D. 2012 Influence of an anisotropic slip-length boundary condition on turbulent channel flow. Phys. Fluids 24, 055111.CrossRefGoogle Scholar
Busse, A. & Sandham, N. D. 2013 Turbulent flow over superhydrophobic surfaces – roughness versus slip. In Proceedings of the 14th European Turbulence Conference, Lyon, France.Google Scholar
Cassie, A. B. D. & Baxter, S. 1944 Wettability of porous surfaces. Trans. Faraday Soc. 40, 546–551.CrossRefGoogle Scholar
Choi, C.-H. & Kim, C.-J. 2006 Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96, 066001.CrossRefGoogle Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.CrossRefGoogle Scholar
Choi, C.-H., Ulmanella, U., Kim, J., Ho, C.-M. & Kim, C.-J. 2006 Effective slip and friction reduction in nanograted superhydrophobic microchannels. Phys. Fluids 18, 087105.CrossRefGoogle Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.CrossRefGoogle Scholar
Daniello, R., Waterhouse, N. E. & Rothstein, J. P. 2009 Turbulent drag reduction using superhydrophobic surfaces. Phys. Fluids 21, 085103.CrossRefGoogle Scholar
Freund, J. B. 2003 The atomic detail of a wetting/de-wetting flow. Phys. Fluids 15, L33–L36.CrossRefGoogle Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18, 051703.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011a Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369, 1412–1427.Google ScholarPubMed
García-Mayoral, R. & Jiménez, J. 2011b Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.CrossRefGoogle Scholar
García-Mayoral, R. & Jiménez, J. 2012 Scaling of turbulent structures in riblet channels up to $Re_{{\it\tau}}\approx 550$ . Phys. Fluids 24, 105101.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Hyväluoma, J. & Harting, J. D. R. 2008 Slip flow over structured surfaces with entrapped microbubbles. Phys. Rev. Lett. 100, 246001.CrossRefGoogle ScholarPubMed
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26, 095102.Google Scholar
Jiménez, J. 1994 On the structure and control of near wall turbulence. Phys. Fluids 6 (2), 944–953.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Jiménez, J., Uhlman, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Kamrin, K., Bazant, M. Z. & Stone, H. A. 2010 Effective slip boundary conditions for arbitrary periodic surfaces: the surface mobility tensor. J. Fluid Mech. 658, 409–437.CrossRefGoogle Scholar
Karatay, E., Haase, A. S., Visser, C. W., Sun, C., Lohse, D., Tsaia, P. A. & Lammertink, R. G. H. 2013 Control of slippage with tunable bubble mattresses. Proc. Natl Acad. Sci. USA 110 (21), 8422–8426.CrossRefGoogle ScholarPubMed
Kim, J. & Moin, P. 1985 Application of a fractional step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Lauga, J. & Stone, H. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.CrossRefGoogle Scholar
Lee, C. & Kim, C.-J. 2009 Maximizing the giant liquid slip on superhydrophobic microstructures by nanostructuring their sidewalls. Langmuir 25, 12812–12818.CrossRefGoogle ScholarPubMed
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_{{\it\tau}}=5200$ . J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to $Re_{{\it\tau}}=4200$ . Phys. Fluids 26, 011702.CrossRefGoogle Scholar
Luchini, P. 1996 Reducing the turbulent skin friction. In Computational Methods in Applied Sciences ‘96 (ed. Desideri, J.-A. et al. ), pp. 466–470. Wiley.Google Scholar
Luchini, P., Manzo, F. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.CrossRefGoogle Scholar
Martell, M. B., Rothstein, J. P. & Perot, J. B. 2010 An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 22, 065102.CrossRefGoogle Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16, L55–L58.CrossRefGoogle Scholar
Min, T. & Kim, J. 2005 Effects of hydrophobic surface on stability and transition. Phys. Fluids 17, 108106.CrossRefGoogle Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143, 90–124.CrossRefGoogle Scholar
Moser, R., Kim, J. & Mansour, N. 1998 Direct numerical simulation of turbulent channel flow up to $Re_{{\it\tau}}\approx 590$ . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Ou, J., Perot, J. B. & Rothstein, J. P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635–4643.CrossRefGoogle Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.CrossRefGoogle Scholar
Park, H., Sun, G. & Kim, C.-J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.CrossRefGoogle Scholar
Patankar, N. A. 2010 Consolidation of hydrophobic transition criteria by using an approximate energy minimization approach. Langmuir 26, 8941–8945.CrossRefGoogle ScholarPubMed
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.CrossRefGoogle Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.CrossRefGoogle Scholar
Samaha, M. A., Vahedi, T. H. & Gad-el-Hak, M. 2011 Modeling drag reduction and meniscus stability of superhydrophobic surface of random roughness. Phys. Fluids 23, 012001.CrossRefGoogle Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2013 Pressure fluctuations in turbulent flows over superhydrophobic surfaces. CTR Ann. Res. Briefs 2013, 217–229.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2014 Turbulent flows over superhydrophobic surfaces: gas–liquid interface dynamics. In Proceedings of the 30th Symposium on Naval Hydrodynamics, Hobart, Australia.Google Scholar
Spalart, P. R. & McLean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. Lond. A 369, 1556–1569.Google ScholarPubMed
Srinivasan, S., Kleingartner, J. A., Gilbert, J. B., Cohen, R. E., Milne, A. J. B. & McKinley, G. H. 2015 Sustainable drag reduction in turbulent Taylor–Couette flows by depositing sprayable superhydrophobic surfaces. Phys. Rev. Lett. 114, 014501.CrossRefGoogle ScholarPubMed
Steinberger, A., cile Cottin-Bizonne, C., Kleimann, P. & Charlaix, E. 2007 High friction on a bubble mattress. Nat. Mater. 6, 665–668.CrossRefGoogle ScholarPubMed
Teo, C. J. & Khoo, B. C. 2010 Flow past superhydrophobic surfaces containing longitudinal grooves: effects of interface curvature. Microfluid. Nanofluid. 9, 499–511.CrossRefGoogle Scholar
Thompson, P. A. & Troian, S. M. 1997 A general boundary condition for liquid flow at solid surfaces. Nature 389, 360–362.CrossRefGoogle Scholar
Türk, S., Daschiel, G., Stroh, A., Hasegawa, Y. & Frohnapfel, B. 2014 Turbulent flow over superhydrophobic surfaces with streamwise grooves. J. Fluid Mech. 747, 186–217.CrossRefGoogle Scholar
Van Dyke, Milton 1962 Higher approximations in boundary-layer theory. Part 1. General analysis. J. Fluid Mech. 14, 161–177.CrossRefGoogle Scholar
Watanabe, K., Yanuar & Udagawa, H. 1999 Drag reduction of newtonian fluid in a circular pipe with highly water-repellent wall. J. Fluid Mech. 381, 225–238.CrossRefGoogle Scholar
Wenzel, R. N. 1936 Resistance of solid surfaces to wetting by water. Ind. Engng Chem. 28, 988–994.CrossRefGoogle Scholar
Woolford, B., Prince, J., Maynes, D. & Webb, B. W. 2009 Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls. Phys. Fluids 21, 085106.CrossRefGoogle Scholar
Ybert, C., Barentin, C. & Cottin-Bizonne, C. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19, 123601.CrossRefGoogle Scholar

Seo et al. supplementary movie

Instantaneous wall-normal vorticity contours at y=0 for case P13.

Download Seo et al. supplementary movie(Video)
Video 18 MB

Seo et al. supplementary movie

Instantaneous wall-normal vorticity contours at y=0 for case P13.

Download Seo et al. supplementary movie(Video)
Video 6.9 MB

Seo et al. supplementary movie

Instantaneous wall-normal vorticity contours at y=0 for case P26.

Download Seo et al. supplementary movie(Video)
Video 16.7 MB

Seo et al. supplementary movie

Instantaneous wall-normal vorticity contours at y=0 for case P26.

Download Seo et al. supplementary movie(Video)
Video 8.1 MB

Seo et al. supplementary movie

Instantaneous wall-normal vorticity contours at y=0 for case P39.

Download Seo et al. supplementary movie(Video)
Video 16.3 MB

Seo et al. supplementary movie

Instantaneous wall-normal vorticity contours at y=0 for case P39.

Download Seo et al. supplementary movie(Video)
Video 7.8 MB

Seo et al. supplementary movie

Instantaneous pressure contours at y=0 for case P39.

Download Seo et al. supplementary movie(Video)
Video 12.4 MB

Seo et al. supplementary movie

Instantaneous pressure contours at y=0 for case P39.

Download Seo et al. supplementary movie(Video)
Video 8.1 MB

Seo et al. supplementary movie

Instantaneous pressure contours at y=0 for case P13.

Download Seo et al. supplementary movie(Video)
Video 16.1 MB

Seo et al. supplementary movie

Instantaneous pressure contours at y=0 for case P13.

Download Seo et al. supplementary movie(Video)
Video 8.4 MB

Seo et al. supplementary movie

Instantaneous pressure contours at y=0 for case P26.

Download Seo et al. supplementary movie(Video)
Video 16.5 MB

Seo et al. supplementary movie

Instantaneous pressure contours at y=0 for case P26.

Download Seo et al. supplementary movie(Video)
Video 7.9 MB