Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T13:15:58.395Z Has data issue: false hasContentIssue false
  • English
  • Français

Predictive control of spiral vortex breakdown

Published online by Cambridge University Press:  06 March 2018

S. Pasche Open the ORCID record for S. Pasche [Opens in a new window] ,
F. Gallaire Open the ORCID record for F. Gallaire [Opens in a new window]  and
F. Avellan
S. Pasche*
Affiliation:
Laboratory for Hydraulic Machines, École Polytechnique Fédérale de Lausanne, CH-1007 Lausanne, Switzerland
F. Gallaire
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
F. Avellan
Affiliation:
Laboratory for Hydraulic Machines, École Polytechnique Fédérale de Lausanne, CH-1007 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

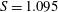The predictive control of the self-sustained single spiral vortex breakdown mode is addressed in the three-dimensional flow geometry of Ruith et al. (2003) for a constant swirl number $S=1.095$. Based on adjoint optimization algorithms, two different control strategies have been designed. First, a quadratic objective function minimizing the radial velocity intensity, taking advantage of the physical mechanism underpinning spiral vortex breakdown. The second strategy focuses on the hydrodynamic instability properties using as objective function the growth rate of the most unstable global eigenmode. These minimization algorithms seek for an optimal volume force in an axisymmetric domain avoiding therefore expensive three-dimensional computations. In addition to considering eigenvalues around the base flow, we also investigate the stability around the mean flow and we find that it correctly predicts the frequency of the self-sustained single spiral vortex breakdown mode for Reynolds numbers up to $Re=500$. Close to the instability threshold, at a Reynolds value of 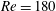$Re=180$, all these control strategies successfully quench the spiral vortex breakdown. The related volume force is found identical for the base and mean flow eigenvalue control even if the uncontrolled growth rates differ significantly. The control of the least unstable eigenvalue of the mean flow is not only found optimal at 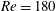$Re=180$, it also stabilizes the flow at a Reynolds value as large as 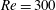$Re=300$, which opens promising extensions to industrial applications.

JFM classification

Flow Control: Flow Control Instability: Instability Vortex Flows: Vortex breakdown
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 58 - 86
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Althaus, W., Krause, E., Hofhaus, J. & Weimer, M. 1994 Vortex breakdown: transition between bubble- and spiral-type breakdown. Meccanica 29 (4), 373–382.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750.CrossRefGoogle Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.CrossRefGoogle Scholar
Bewley, T. R. & Liu, S. 1998 Optimal and robust control and estimation of linear paths to transition. J. Fluid Mech. 365, 305–349.CrossRefGoogle Scholar
Bewley, T. R., Moin, P. & Temam, R. 2001 DNS-based predictive control of turbulence: an optimal benchmark for feedback algorithms. J. Fluid Mech. 447, 179–225.CrossRefGoogle Scholar
Boujo, E. & Gallaire, F. 2014 Controlled reattachment in separated flows: a variational approach to recirculation length reduction. J. Fluid Mech. 742, 618–635.CrossRefGoogle Scholar
Camarri, S. & Iollo, A. 2010 Feedback control of the vortex-shedding instability based on sensitivity analysis. Phys. Fluids 22, 094102.CrossRefGoogle Scholar
Carini, M., Airiau, C., Debien, A. & Pralits, J. O. 2017 Global stability and control of the confined turbulent flow past a thick flat plate. Phys. Fluids 29 (2), 024102.Google Scholar
Delbende, I., Chomaz, J.-C. & Huerre, P. 1998 Absolute/convective instabilities in the batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.Google Scholar
Escudier, M. P. & Zehnder, N. 1982 Vortex-flow regimes. J. Fluid Mech. 115, 105–121.Google Scholar
European, Commissions2017 European policy: Climate strategies and targets.Google Scholar
Favrel, A., Müller, A., Landry, C., Yamamoto, K. & Avellan, F. 2015 Study of the vortex induced pressure excitation source in a Francis turbine draft tube by particle image velocimetry. Exp. Fluids 56 (215), 1–15.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 Web page. http://nek5000.mcs.anl.gov.Google Scholar
Gallaire, F. & Chomaz, J.-C. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.Google Scholar
Gallaire, F., Chomaz, J.-C. & Huerre, P. 2004 Closed-loop control of vortex breakdown: a model study. J. Fluid Mech. 511, 67–93.Google Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Goit, J. P. & Meyers, J. 2015 Optimal control of energy extraction in wind-farm boundary layers. J. Fluid Mech. 768, 5–50.CrossRefGoogle Scholar
Grabowski, W. J. & Berger, S. A. 1976 Solutions of the Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75 (3), 525–544.Google Scholar
Grimble, T. A., Agarwal, A. & Juniper, M. P. 2017 Local linear stability analysis of cyclone separators. J. Fluid Mech. 816, 507–538.Google Scholar
Gunzburger, M. D. 1999 Sensitivities, adjoints and flow optimization. Intl J. Numer. Mech. Fluids 31, 53–78.Google Scholar
Gursul, I., Wang, Z. & Vardaki, E. 2007 Review of flow control mechanisms of leading-edge vortices. Prog. Aerosp. Sci. 43 (7), 246–270.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.CrossRefGoogle Scholar
Hecht, F. 2012 New development in freefem++. J. Numer. Math. 20 (3–4), 251–265.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Joslin, R., Gunzburger, M., Nicolaides, R., Erlebacher, G. & Hussaini, M. 1997 Self-contained automated methodology for optimal flow control. AIAA J. 35 (5), 816–824.CrossRefGoogle Scholar
Khorrami, M. R. 1991 A Chebyshev spectral collocation method using a staggered grid for the stability of cylindrical flows. Intl J. Numer. Meth. Fluids 12, 825–833.Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.Google Scholar
Lacis, U., Brosse, N., Ingremeau, F., Mazzino, A., Lundell, F., Kellay, H. & Bagheri, S. 2014 Passive appendages generate drift through symmetry breaking. Nat. Commun. 5 (5310), 1–9.Google Scholar
Lambourne, N. C. & Bryer, D. W. 1962 The bursting of leading-edge vortices – some observations and discussion of the phenomenon. Aero. Res. Counc. 3292, 1–35.Google Scholar
Leibovich, S. 1978 The structure of the vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.CrossRefGoogle Scholar
Lions, J. L. 1971 Optimal Control of Systems Governed by Partial Differential Equations. Springer.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.CrossRefGoogle Scholar
Mantič-Lugo, V., Arratia, C. & Gallaire, F. 2014 Self-consistent mean flow description of the nonlinear saturation of the vortex shedding in the cylinder wake. Phys. Rev. Lett. 113, 084501.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Marston, J. B., Chini, G. P. & Tobias, S. M. 2016 Generalized quasilinear approximation: application to zonal jets. Phys. Rev. Lett. 116, 214501.Google Scholar
Maurel, A., Pagneux, V. & Wesfreid, J. E. 1995 Mean-flow correction as non-linear saturation mechanism. Europhys. Lett. 32 (3), 217.Google Scholar
Meliga, P. & Gallaire, F. 2011 Control of axisymmetric vortex breakdown in a constricted pipe: nonlinear steady states and weakly nonlinear asymptotic expansions. Phys. Fluids 23 (8), 084102.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012a A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Meliga, P., Pujals, G. & Serre, E. 2012b Sensitivity of 2-d turbulent flow past a d-shaped cylinder using global stability. Phys. Fluids 24 (6), 061701.Google Scholar
Mettot, C., Sipp, D. & Bézard, H. 2014 Quasi-laminar stability and sensitivity analyses for turbulent flows prediction of low-frequency unsteadyness and passive control. Phys. Fluids 26 (4), 045112.Google Scholar
Nishi, M. & Liu, S. 2013 An outlook on the draft tube surge study. Intl J. Fluid Mach. Syst. 6, 33–48.Google Scholar
Oberleithner, K., Sthr, M., Im, S. H., Arndt, C. M. & Steinberg, A. M. 2015 Formation and flame-induced suppression of the precessing vortex core in a swirl combustor: experiments and linear stability analysis. Combust. Flame 162 (8), 3100–3114.Google Scholar
Paredes, P., Terhaar, S., Oberleithner, K., Theofilis, V. & Passchereit, C. O. 2015 Global and local hydrodynamic stability analysis as a tool for combustor dynamics modeling. Trans. ASME J. Engng Gas Turbines Power 138 (2), 021504–021504–7.Google Scholar
Pasche, S.2018 Dynamics and optimal control of self-sustained instabilities in laminar and turbulent swirling flows: application to the part load vortex rope in Francis turbines. PhD thesis, École Polytechnique Fédérale de Lausanne.Google Scholar
Pasche, S., Avellan, F. & Gallaire, F. 2017 Part load vortex rope as a global unstable mode. Trans. ASME J. Fluids Engng 139, 051102–11.Google Scholar
Paschereit, C. O., Flohr, P. & Gutmark, E. J. 2002 Combustion control by vortex breakdown stabilization. J. Turbomach. 128, 679–688.Google Scholar
Passaggia, P-Y. & Ehrenstein, U. 2013 Adjoint based optimization and control of a separated boundary-layer flow. Eur. J. Mech. (B/Fluids) 41, 169–177.Google Scholar
Polak, E. 1997 Optimization Algorithms and Consistent Approximations. Springer.Google Scholar
Polak, E. & Ribiere, G. 1969 Note sur la convergence de méthodes de directions conjuguées. ESAIM: Mathematical Modelling and Numerical Analysis – Modélisation Mathématique et Analyse Numérique 3 (R1), 35–43.Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.CrossRefGoogle Scholar
Rheingans, W. J. 1940 Power swings in hydroelectric power plants. Trans. ASME 62 (174), 171–184.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
Rusak, Z., Granata, J. & Wang, S. 2015 An active feedback flow control theory of the axisymmetric vortex breakdown process. J. Fluid Mech. 774, 488–528.CrossRefGoogle Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45 (3), 545–559.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Spall, R. E., Gatski, T. B. & Ash, R. L. 1990 The structure and dynamics of bubble-type vortex breakdown. Proc. R. Soc. Lond. A 429 (1877), 613–637.Google Scholar
Squire, H. B. 1960 Analysis of the Vortex Breakdown Phenomenon. Imperial College of Science and Technology, Aeronautics Department.Google Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex shedding at low Reynolds numbers. J. Fluid Mech. 218, 71–107.Google Scholar
Susan-Resiga, R., Muntean, S., Hasmatuchi, V., Anton, I. & Avellan, F. 2010 Analysis and prevention of vortex breakdown in the simplified discharge cone of a Francis turbine. J. Fluids Engng 132 (5), 051102.Google Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (pvc) in swirl combustion systems. Prog. Energy Combust. Sci. 32 (2), 93–161.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Vyazmina, E., Nichols, J. W., Chomaz, J.-M. & Schmid, P. J. 2009 The bifurcation structure of viscous steady axisymmetric vortex breakdown with open lateral boundaries. Phys. Fluids 21 (7), 074107.Google Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar