Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T07:24:01.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On the maximal spreading of impacting compound drops

Published online by Cambridge University Press:  12 September 2018

H.-R. Liu ,
C.-Y. Zhang ,
P. Gao Open the ORCID record for P. Gao [Opens in a new window] ,
X.-Y. Lu Open the ORCID record for X.-Y. Lu [Opens in a new window]  and
H. Ding Open the ORCID record for H. Ding [Opens in a new window]
H.-R. Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
C.-Y. Zhang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
P. Gao
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230027, China
X.-Y. Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
H. Ding*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230027, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We numerically study the impact of a compound drop on a hydrophobic substrate using a ternary-fluid diffuse-interface method, aiming to understand how the presence of the inner droplet affects the spreading dynamics and maximal spreading of the compound drop. First, it is interesting to see that the numerical results for an impacting pure drop agree well with the universal rescaling of maximal spreading ratio proposed by Lee et al. (J. Fluid Mech., vol. 786, 2016, R4). Second, two flow regimes have been identified for an impacting compound drop: namely jammed spreading and joint rim formation. The maximal spreading ratio of the compound drop is found to depend on the volume fraction of the inner droplet $\unicode[STIX]{x1D6FC}$, the surface tension ratio 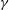$\unicode[STIX]{x1D6FE}$, the Weber number and the flow regime. 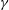Moreover, we propose a universal rescaling of maximal spreading ratio for compound drops, by integrating the one for pure drops with a corrected Weber number that takes $\unicode[STIX]{x1D6FC}$, $\unicode[STIX]{x1D6FE}$ and the flow regime into account. The predictions of the universal rescaling are in good agreement with the numerical results for impacting compound drops.

JFM classification

Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , R6
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chandra, B. S. & Avedisian, C. T. 1991 On the collision of a droplet with a solid surface. Proc. R. Soc. Lond. A 432, 13–41.Google Scholar
Chen, R. H., Chiu, S. L. & Lin, T. H. 2007 Resident time of a compound drop impinging on a hot surface. Appl. Therm. Engng 27, 2079–2085.Google Scholar
Chiu, S. & Lin, T. 2005 Experiment on the dynamics of a compound drop impinging on a hot surface. Phys. Fluids 17, 122103.Google Scholar
Clanet, C., Béguin, C., Richard, D. & Quéué, D. 2004 Maximal deformation of an impacting drop. J. Fluid Mech. 517, 199–208.Google Scholar
Collings, E. W., Markworth, A. J., Mccoy, J. K. & Saunder, J. H. 1991 Splat-quench solidification of freely falling liquid-metal drops by impact on a planar substrate. J. Mater. Sci. 25, 3677–3682.Google Scholar
Delcea, M., Mohwald, H. & Skirtach, A. G. 2011 Stimuli-responsive LbL capsules and nanoshells for drug delivery. Adv. Drug Deliv. Rev. 63, 730–747.Google Scholar
Derby, B. 2010 Inkjet printing of functional and structural materials: fluid property requirements feature stability, and resolution. Annu. Rev. Mater. Res. 40, 395–414.Google Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22, 062101.Google Scholar
Gulyaev, I. P. & Solonenko, O. P. 2013 Hollow droplets impacting onto a solid surface. Exp. Fluids 54, 1432.Google Scholar
Hendriks, J., Visser, C. W., Henke, S., Leijten, J., Saris, D. B. F., Sun, C., Lohse, D. & Karperien, M. 2015 Optimizing cell viability in droplet-based cell deposition. Sci. Rep. 5, 11304.Google Scholar
Joung, Y. S. & Buie, C. R. 2014 Aerosol generation by raindrop impact on soil. Nat. Commun. 6, 6083.Google Scholar
Laan, N., Bruin, K. G., Bartolo, D., Josserand, C. & Bonn, D. 2014 Maximum diameter of impacting liquid droplets. Phys. Rev. Appl. 2, 044018.Google Scholar
Lee, J. B., Laan, N., De Bruin, K. G., Skantzaris, G., Shahidzadeh, N., Derome, D., Carmeliet, J. & Bonn, D. 2016 Universal rescaling of drop impact on smooth and rough surfaces. J. Fluid Mech. 786, R4.Google Scholar
Li, D., Duan, X., Zheng, Z. & Liu, Y. 2018 Dynamics and heat transfer of a hollow droplet impact on a wetted solid surface. Intl J. Heat Mass Transfer 122, 1014–1023.Google Scholar
Liu, H. R. & Ding, H. 2015 A diffuse-interface immersed-boundary method for two-dimensional simulation of flows with moving contact lines on curved substrates. J. Comput. Phys. 294, 484–502.Google Scholar
Mishchenko, L., Hatton, B., Bahadur, V., Taylor, J. A., Krupenkin, T. & Aizenberg, J. 2010 Design of ice-free nanostructured impacting water droplets. ACS Nano 4, 7699–7707.Google Scholar
Moreira, A. L. N., Moita, A. S. & Panao, M. R. 2010 Advances and challenges in explaining fuel spray impingement: How much of single droplet impact research is useful? Prog. Energ. Combust. 36, 554–580.Google Scholar
Murphy, S. V. & Atala, A. 2014 3D bioprinting of tissues and organs. Nat. Biotechnol. 32, 773–785.Google Scholar
Tasoglu, S., Kaynak, G., Szer, A. J., Demirci, U. & Muradoglu, M. 2010 Impact of a compound droplet on a flat surface: a model for single cell epitaxy. Phys. Fluids 22, 082103.Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K., Ootsuka, N. & Hatsuki, Y. 2005 The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 545, 203–212.Google Scholar
Wildeman, S., Visser, C. W., Sun, C. & Lohse, D. 2016 On the spreading of impacting drops. J. Fluid Mech. 805, 636–656.Google Scholar
Zhang, C. Y., Ding, H., Gao, P. & Wu, Y. L. 2016 Diffuse interface simulation of ternary fluids in contact with solid. J. Comput. Phys. 309, 37–51.Google Scholar