Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T02:43:55.807Z Has data issue: false hasContentIssue false
  • English
  • Français

On the heat transferred to the air surrounding a semi-infinite inclined hot plate

Published online by Cambridge University Press:  02 September 2013

Michael J. Gollner ,
Antonio L. Sánchez  and
Forman A. Williams
Michael J. Gollner*
Affiliation:
Department of Fire Protection Engineering, University of Maryland, College Park, 3106 J.M. Patterson Building, College Park, MD 20742-3031, USA
Antonio L. Sánchez
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, San Diego, 9500 Gilman Dr., La Jolla, CA 92093-0411, USA Department of Thermal and Fluids Engineering, Universidad Carlos III de Madrid, Leganés, 28911, Spain
Forman A. Williams
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, San Diego, 9500 Gilman Dr., La Jolla, CA 92093-0411, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An asymptotic analysis of laminar free convection in a boundary layer over an isothermal semi-infinite flat plate inclined at some angle to the vertical has been performed. Existing analytical solutions show no difference in the heat-transfer rate between the upper and lower surfaces of the plate, contrary to observations. To investigate this, higher-order perturbations of the non-dimensional temperature, velocity and pressure across the boundary layer were computed and found to show only small variations from first-order perturbations previously reported. Unexpectedly, third-order perturbations of all functions were found to be identical to those of the vertical plate, indicating that differences in temperature between both sides of the plate are limited to exceedingly small terms of order 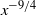${x}^{- 9/ 4} $ or smaller, $x$ being the distance from the leading edge, non-dimensionalized by the buoyancy length scale. Dominant differences between heat-transfer rates on the upper and lower surfaces were therefore concluded to be due to near-leading-edge effects. In applying an integral form of the conservation equations to the near-leading-edge region, it was found that, up to terms of order unity in $x$, the total heat-exchange rate for the inclined plate is identical to that of the vertical plate, so that the heat-transfer gain on one side balances exactly the loss occurring on the other. This simplification allowed determination of an upper bound for differences in heat-transfer rates between the upper and lower sides, even though complete determination of the differences would require a numerical integration of the full Navier–Stokes equations near the leading edge of the plate.

JFM classification

Boundary Layers: Boundary Layers Compressible Flows: Compressible boundary layers Compressible Flows: Compressible Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 304 - 315
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Clarke, J. F. 1973 Transpiration and natural convection: the vertical-flat-plate problem. J. Fluid Mech. 57, 45–61.Google Scholar
Fernandez-Pello, A. C. & Hirano, T. 1978 Controlling mechanisms of flame spread. Combust. Flame 31, 135–148.Google Scholar
Gollner, M. J., Huang, X., Cobian, J., Rangwala, A. S. & Williams, F. A. 2013 Experimental study of upward flame spread of an inclined fuel surface. Proc. Combust. Inst. 34 (2), 2531–2538.Google Scholar
Imai, I. 1957 Second approximation to the laminar boundary layer flow over a flat plate. J. Aero. Sci. 24, 155–156.Google Scholar
Jones, D. R. 1973 Free convection from a semi-infinite flat plate inclined at a small angle to the horizontal. Q. J. Mech. Appl. Math. 26, 77–98.Google Scholar
Kierkus, W. T. 1968 An analysis of laminar free convection flow and heat transfer about an inclined isothermal plate. Intl. J. Heat Mass Transfer 11, 241–253.Google Scholar
Messiter, A. F. & Liñán, A. 1976 The vertical plate in laminar free convection: effects of leading and trailing edges and discontinuous temperature. J. Appl. Math. Phys. (ZAMP) 27, 633–651.Google Scholar
Riley, N. 1975 Note on a paper by Kierkus. Intl J. Heat Mass Transfer 18, 991–993.Google Scholar