Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-19T14:04:35.316Z Has data issue: false hasContentIssue false
  • English
  • Français

On generation of sound in wall-bounded shear flows: back action of sound and global acoustic coupling

Published online by Cambridge University Press:  15 November 2011

Xuesong Wu
Xuesong Wu*
Affiliation:
Department of Mechanics, Tianjin University, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In two previous papers (Wu, J. Fluid Mech., vol. 453, 2002, p. 289, and Wu & Hogg, J. Fluid Mech., vol. 550, 2006, p. 307), a formal asymptotic procedure was developed to calculate the sound radiated by unsteady boundary-layer flows that are described by the triple-deck theory. That approach requires lengthy calculations, and so is now improved to construct a simpler composite theory, which retains the capacity of systematically identifying and approximating the relevant sources, but also naturally includes the effect of mean-flow refraction and more importantly the back action of the emitted sound on the source itself. The combined effect of refraction and back action is represented by an ‘impedance coefficient’, and the present analysis yields an analytical expression for this parameter, which was usually introduced on a semi-empirical basis. The expression indicates that for Mach number 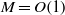, the mean-flow refraction and back action of the sound have a leading-order effect on the acoustic field within the shallow angles to the streamwise directions. A parametric study suggests that the back effect of sound is actually appreciable in a sizeable portion of the acoustic field for 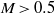, becomes more pronounced, and eventually influences the entire acoustic field in the transonic limit. In the supersonic regime, the acoustic field is characterized by distinctive Mach-wave beams, which exert a leading-order influence on the source. The analysis also indicates that acoustic radiation in the subsonic and supersonic regimes is fundamentally different. In the subsonic regime, the sound is produced by small-wavenumber components of the hydrodynamic motion, and can be characterized by acoustic multipoles, whereas in the supersonic regime, broadband finite-wavenumber components of the hydrodynamic motion contribute and the concept of a multipolar source becomes untenable. The global acoustic feedback loop is investigated using a model consisting of two well-separated roughness elements, in which the sound wave emitted due to the scattering of a Tollmien–Schlichting (T–S) wave by the downstream roughness propagates upstream and impinges on the upstream roughness to regenerate the T–S wave. Numerical calculations suggest that at high Reynolds numbers and for moderate roughness heights, the long-range acoustic coupling may lead to global instability, which is characterized by self-sustained oscillations at discrete frequencies. The dominant peak frequency may jump from one value to another as the Reynolds number or the distance between the roughness elements is varied gradually.

JFM classification

Acoustics: Aeroacoustics Boundary Layers: Boundary layer receptivity Boundary Layers: Boundary layer stability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 689 , 25 December 2011 , pp. 279 - 316
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Argawal, A., Morris, P. J. & Mani, R. 2004 Sound propagation in non-uniform flow: suppression of instability waves. AIAA J. 42 (1), 80–88.Google Scholar
2. Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions. National Bureau of Standards.Google Scholar
3. Arbey, H. & Bataille, J. 1983 Noise generated by aerofoil placed in a uniform laminar flow. J. Fluid Mech. 134, 33–47.Google Scholar
4. Bowles, R. I. & Smith, F. T. 1993 On boundary-layer transition in transonic flow. J. Engng Math. 27, 309–342.CrossRefGoogle Scholar
5. Clark, L. T. 1971 The radiation of sound from an aerofoil immersed in a laminar flow. Trans. ASME J. Engng Power 93, 366–376.CrossRefGoogle Scholar
6. Colonius, T., Lele, S. K. & Moin, P. 1997 Sound generation in a mixing layer. J. Fluid Mech. 330, 375–409.CrossRefGoogle Scholar
7. Crighton, D. G. 1981 Acoustics as a branch of fluid mechanics. J. Fluid Mech. 106, 261–298.CrossRefGoogle Scholar
8. Crighton, D. G. 1988 Goals for computational aeroacoustics. In Computational Acoustics: Algorithms and Applications (ed. Lee, D., Sternberg, R. L. & Schultz, M. H. ), pp. 3–20. Elsevier.Google Scholar
9. Crighton, D. G. 1991 Airframe noise. In Aeroacoustics of Flight Vehicles: Theory and Practice (ed. Hubbard, H. H. ). vol. 1: Noise Sources , pp. 391–447. NASA.Google Scholar
10. Crighton, D. G. 1993 Computational aeroacoustics for low Mach number flows. In Computational Aeroacoustics (ed. Hardin, J. C. & Hussaini, M. Y. ), pp. 50–68. Springer.Google Scholar
11. Crow, S. C. 1970 Aerodynamic sound emission as a singular perturbation problem. Stud. Appl. Math. 49, 21–44.CrossRefGoogle Scholar
12. Curle, N. 1955 The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. A 231, 505–514.Google Scholar
13. Desquesnes, G., Terracol, M. & Sagaut, P. 2007 Numerical investigation of the tone noise mechanism over laminar aerofoils. J. Fluid Mech. 591, 155–182.CrossRefGoogle Scholar
14. Ffowcs Williams, J. E. & Maidanik, G. 1965 The Mach wave field radiated by supersonic turbulent shear flows. J. Fluid Mech. 21, 641–657.Google Scholar
15. Freund, J. B., Lele, S. K. & Wei, M. 2005 The robustness of acoustic analogies. In Proceedings of the Summer Programme 2004, Center for Turbulence Research, Stanford, pp. 241–252.Google Scholar
16. Goldstein, M. E. 1983 The evolution of Tollmien–Schlichting waves near a leading edge. J. Fluid Mech. 127, 59–81.Google Scholar
17. Goldstein, M. E. 1984 Aeroacoustics of turbulent shear flows. Annu. Rev. Fluid Mech. 16, 263–285.Google Scholar
18. Goldstein, M. E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–529.Google Scholar
19. Goldstein, M. E. 2003 A generalized acoustic analogy. J. Fluid Mech. 488, 315–333.Google Scholar
20. Goldstein, M. E. & Leib, S. J. 2005 The role of instability waves in predicting jet noise. J. Fluid Mech. 525, 37–72.Google Scholar
21. Hogg, L. W. 2005 Asymptotic approach to aeroacoustics. PhD thesis, University of London.Google Scholar
22. Howe, M. S. 1975 Contributions to the theory of aerodynamic sound, with application to excess jet noise and the theory of the flute. J Fluid Mech. 71, 625–673.Google Scholar
23. Howe, M. S. 1979 The role of surface shear stress fluctuations in the generation of boundary layer noise. J. Sound Vib. 65, 159–164.CrossRefGoogle Scholar
24. Karabasov, S. A., Afsar, M. Z., Hynes, T. P., Dowling, A. P., McMullan, W. A., Pokora, C. D., Page, G. I. & McGuirk, J. J. 2010 Jet noise: acoustic analogy informed by large eddy simulation. AIAA J. 48 (7), 1312–1325.Google Scholar
25. Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2010 Stability and receptivity characteristics of a laminar separation bubble on a aerofoil. J. Fluid Mech. 648, 257–296.Google Scholar
26. Lighthill, M. J. 1952 On sound generated aerodynamically. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
27. Leib, S. J. & Goldstein, M. E. 2011 Hybrid source model for predicting high-speed jet noise. AIAA J. 49 (7), 1324–1335.Google Scholar
28. Lilley, G. M. 1974 On the noise from jets, noise mechanisms. AGARD-CP-131, pp. 13.1–13.12.Google Scholar
29. Mani, R. 1976 The influence of jet flow on jet noise. Part 1. The noise of unheated jets. J. Fluid Mech. 73, 753–778.Google Scholar
30. Nash, E. C., Lowson, M. V. & McAlpine, A. 1999 Boundary-layer instability noise on aerofoils. J. Fluid Mech. 382, 27–61.Google Scholar
31. Obermeier, F. 1967 Berechnung aerodynamisch erzeugter Schallfelder mittels der Methode der ‘Matched Asymptotic Expansions’. Acustica 18, 238–240.Google Scholar
32. Phillips, O. M. 1960 On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 9, 1–27.CrossRefGoogle Scholar
33. Pierce, A. D. 1989 Acoustics: An Introduction to its Physical Principles and Applications. The Acoustic Society of America.Google Scholar
34. Rockwell, D. & Naudasher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11, 67–94.CrossRefGoogle Scholar
35. Ruban, A. I. 1984 On Tollmien–Schlichting wave generation by sound (in Russian). Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 5, 44 (translation Fluid Dyn. 19, 709–716).Google Scholar
36. Sandberg, R. D. & Sandham, N. D. 2007 Direct numerical simulation of turbulent flow past a trailing edge and the associated noise generation. J. Fluid Mech. 596, 353–385.Google Scholar
37. Shariff, K. & Wang, M 2005 A numerical experiment to determine whether surface shear-stress fluctuations are a true sound source. Phys. Fluids 17, 107105.CrossRefGoogle Scholar
38. Suzuki, T. & Lele, S. K. 2003 Green’s function for a source in a boundary layer: direct waves, channelled waves and diffracted waves. J. Fluid Mech. 477, 129–173.Google Scholar
39. Smith, F. T. 1973 Laminar flow over a small hump on flat plate. J. Fluid Mech. 57, 803–824.Google Scholar
40. Smith, F. T. 1979 On the non-parallel flow stability of the Blasius boundary layer. Proc. R. Soc. Lond. A 366, 91–109.Google Scholar
41. Smith, F. T. 1989 On the first-mode instability in subsonic, supersonic or hypersonic boundary layers. J. Fluid Mech. 198, 127–153.CrossRefGoogle Scholar
42. Stewartson, K. 1974 Multistructured boundary layers of flat plates and related bodies. Adv. Appl. Mech. 14, 145–239.Google Scholar
43. Tam, C. K. W. & Burton, D. E. 1984a Sound generated by instability waves of supersonic flow. Part I. Two-dimensional mixing layers. J. Fluid Mech. 138, 249–271.Google Scholar
44. Tam, C. K. W. & Burton, D. E. 1984b Sound generated by instability waves of supersonic flow. Part II. Axisymmetric jets. J. Fluid Mech. 138, 273–295.Google Scholar
45. Timoshin, S. N. 2005 Feedback instability in a boundary-layer flow over roughness. Mathematika 52, 161–168.Google Scholar
46. Wang, M., Freund, J. B. & Lele, S. K. 2006 Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 38, 483–512.CrossRefGoogle Scholar
47. Wei, M. & Freund, J. B. 2006 A noise-controlled free shear flow. J. Fluid Mech. 546, 123–152.Google Scholar
48. Wu, X. 2001 Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances: a second-order asymptotic theory and comparison with experiments. J. Fluid Mech. 431, 91–133.Google Scholar
49. Wu, X. 2002 Generation of sound and instability waves due to unsteady suction and injection. J. Fluid Mech. 453, 289–313.CrossRefGoogle Scholar
50. Wu, X. 2005 Mach wave radiation of nonlinearly evolving supersonic instability modes in shear flows. J. Fluid Mech. 523, 121–159.CrossRefGoogle Scholar
51. Wu, X. & Hogg, L. W. 2006 Acoustic radiation of Tollmien–Schlichting waves as they undergo rapid distortion. J. Fluid Mech. 550, 307–347.Google Scholar
52. Wu, X. & Huerre, P. 2009 Low-frequency sound radiated by a nonlinearly modulated wavepacket of helical modes on a subsonic circular jet. J. Fluid Mech. 637, 173–211.Google Scholar
53. Wu, X. & Zhang, J. 2008 Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 2. Coupling with internal gravity waves via topography. J. Fluid Mech. 595, 409–433.Google Scholar