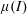Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-09T02:05:10.390Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Stokes’ problem in dense granular media using the $\unicode[STIX]{x1D707}(I)$-rheology

Published online by Cambridge University Press:  23 May 2018

J. John Soundar Jerome Open the ORCID record for J. John Soundar Jerome [Opens in a new window]  and
B. Di Pierro
J. John Soundar Jerome*
Affiliation:
Université de Lyon, Université Claude Bernard Lyon 1, Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS UMR–5509, Boulevard 11 novembre, 69622 Villeurbanne CEDEX, Lyon, France
B. Di Pierro
Affiliation:
Université de Lyon, Université Claude Bernard Lyon 1, Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS UMR–5509, Boulevard 11 novembre, 69622 Villeurbanne CEDEX, Lyon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The classical Stokes’ problem describing the fluid motion due to a steadily moving infinite wall is revisited in the context of dense granular flows of mono-dispersed beads using the recently proposed 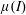$\unicode[STIX]{x1D707}(I)$-rheology. In Newtonian fluids, molecular diffusion brings about a self-similar velocity profile and the boundary layer in which the fluid motion takes place increases indefinitely with time $t$ as 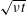$\sqrt{\unicode[STIX]{x1D708}t}$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity. For a dense granular viscoplastic liquid, it is shown that the local shear stress, when properly rescaled, exhibits self-similar behaviour at short time scales and it then rapidly evolves towards a steady-state solution. The resulting shear layer increases in thickness as 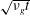$\sqrt{\unicode[STIX]{x1D708}_{g}t}$ analogous to a Newtonian fluid where 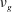$\unicode[STIX]{x1D708}_{g}$ is an equivalent granular kinematic viscosity depending not only on the intrinsic properties of the granular medium, such as grain diameter 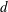$d$, density 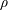$\unicode[STIX]{x1D70C}$ and friction coefficients, but also on the applied pressure 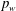$p_{w}$ at the moving wall and the solid fraction 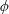$\unicode[STIX]{x1D719}$ (constant). In addition, the 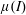$\unicode[STIX]{x1D707}(I)$-rheology indicates that this growth continues until reaching the steady-state boundary layer thickness 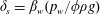$\unicode[STIX]{x1D6FF}_{s}=\unicode[STIX]{x1D6FD}_{w}(p_{w}/\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}g)$, independent of the grain size, at approximately a finite time proportional to 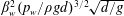$\unicode[STIX]{x1D6FD}_{w}^{2}(p_{w}/\unicode[STIX]{x1D70C}gd)^{3/2}\sqrt{d/g}$, where 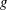$g$ is the acceleration due to gravity and 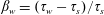$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D70F}_{w}-\unicode[STIX]{x1D70F}_{s})/\unicode[STIX]{x1D70F}_{s}$ is the relative surplus of the steady-state wall shear stress 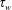$\unicode[STIX]{x1D70F}_{w}$ over the critical wall shear stress 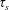$\unicode[STIX]{x1D70F}_{s}$ (yield stress) that is needed to bring the granular medium into motion. For the case of Stokes’ first problem when the wall shear stress 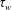$\unicode[STIX]{x1D70F}_{w}$ is imposed externally, the 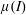$\unicode[STIX]{x1D707}(I)$-rheology suggests that the wall velocity simply grows as 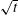$\sqrt{t}$ before saturating to a constant value whereby the internal resistance of the granular medium balances out the applied stresses. In contrast, for the case with an externally imposed wall speed 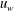$u_{w}$, the dense granular medium near the wall initially maintains a shear stress very close to 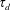$\unicode[STIX]{x1D70F}_{d}$ which is the maximum internal resistance via grain–grain contact friction within the context of the 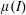$\unicode[STIX]{x1D707}(I)$-rheology. Then the wall shear stress 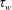$\unicode[STIX]{x1D70F}_{w}$ decreases as 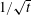$1/\sqrt{t}$ until ultimately saturating to a constant value so that it gives precisely the same steady-state solution as for the imposed shear-stress case. Thereby, the steady-state wall velocity, wall shear stress and the applied wall pressure are related as 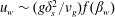$u_{w}\sim (g\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g})f(\unicode[STIX]{x1D6FD}_{w})$ where 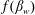$f(\unicode[STIX]{x1D6FD}_{w})$ is either 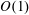$O(1)$ if $\unicode[STIX]{x1D70F}_{w}\sim \unicode[STIX]{x1D70F}_{s}$ or logarithmically large as 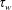$\unicode[STIX]{x1D70F}_{w}$ approaches 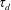$\unicode[STIX]{x1D70F}_{d}$.

JFM classification

Boundary Layers: Boundary layer structure Granular media: Granular media Non-Newtonian Flows: Non-Newtonian Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 365 - 385
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ancey, C. & Bates, B. M. 2017 Stokes’ third problem for Herschel–Bulkley fluids. J. Non-Newtonian Fluid Mech. 243 (Supplement C), 27–37.Google Scholar
Ancey, C., Coussot, P. & Evesque, P. 1999 A theoretical framework for granular suspensions in a steady simple shear flow. J. Rheol. 43 (6), 1673–1699.Google Scholar
Andreotti, B., Forterre, Y. & Pouliquen, O. 2011 Les milieux granulaires: entre fluide et solide. EDP Sciences.Google Scholar
Aranson, I. S. & Tsimring, L. S. 2006 Patterns and collective behavior in granular media: theoretical concepts. Rev. Mod. Phys. 78 (2), 641.CrossRefGoogle Scholar
Baker, J. L., Barker, T. & Gray, J. M. N. T. 2016 A two-dimensional depth-averaged 𝜇(I)-rheology for dense granular avalanches. J. Fluid Mech. 787, 367–395.Google Scholar
Balmforth, N. J., Forterre, Y. & Pouliquen, O. 2009 The viscoplastic Stokes layer. J. Non-Newtonian Fluid Mech. 158 (1), 46–53.Google Scholar
Barker, T. & Gray, J. M. N. T. 2017 Partial regularisation of the incompressible 𝜇(I)-rheology for granular flow. J. Fluid Mech. 828, 5–32.CrossRefGoogle Scholar
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T. 2015 Well-posed and ill-posed behaviour of the 𝜇(I)-rheology for granular flow. J. Fluid Mech. 779, 794–818.Google Scholar
Barker, T., Schaeffer, D. G., Shearer, M. & Gray, J. M. N. T. 2017 Well-posed continuum equations for granular flow with compressibility and 𝜇(I)-rheology. Proc. R. Soc. A 473, 20160846.Google Scholar
Capart, H., Hung, C.-Y. & Stark, C. P. 2015 Depth-integrated equations for entraining granular flows in narrow channels. J. Fluid Mech. 765, R4.Google Scholar
Cawthorn, C. J.2011 Several applications of a model for dense granular flows. PhD thesis, University of Cambridge.Google Scholar
Chauchat, J. & Médale, M. 2014 A three-dimensional numerical model for dense granular flows based on the 𝜇(I)-rheology. J. Comput. Phys. 256, 696–712.Google Scholar
Da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72 (2), 021309.Google Scholar
Devakar, M. & Iyengar, T. K. V. 2008 Stokes problems for an incompressible couple stress fluid. Nonlinear Anal.: Model. Control 1 (2), 181–190.Google Scholar
Devakar, M. & Iyengar, T. K. V. 2009 Stokes’ first problem for a micropolar fluid through state-space approach. Appl. Math. Modell. 33 (2), 924–936.Google Scholar
Ekinci, K. L., Karabacak, D. M. & Yakhot, V. 2008 Universality in oscillating flows. Phys. Rev. Lett. 101, 264501.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.CrossRefGoogle Scholar
Goddard, J. D. & Lee, J. 2017 On the stability of the 𝜇(I) rheology for granular flow. J. Fluid Mech. 833, 302–331.Google Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35 (1), 267–293.Google Scholar
Gray, J. M. N. T. & Edwards, A. N. 2014 A depth-averaged 𝜇(I)-rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 503.Google Scholar
Gray, J. M. N. T., Tai, Y.-C. & Noelle, S. 2003 Shock waves, dead zones and particle-free regions in rapid granular free-surface flows. J. Fluid Mech. 491, 161–181.Google Scholar
Hutter, K. & Rajagopal, K. R. 1994 On flows of granular materials. Contin. Mech. Thermodyn. 6 (2), 81–139.CrossRefGoogle Scholar
Iordanoff, I. & Khonsari, M. M. 2004 Granular lubrication: toward an understanding of the transition between kinetic and quasi-fluid regime. J. Tribol. 126 (1), 137–145.CrossRefGoogle Scholar
Jaeger, H. M., Nagel, S. R. & Behringer, R. P. 1996 Granular solids, liquids, and gases. Rev. Mod. Phys. 68 (4), 1259.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 130, 187–202.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2007 Initiation of granular surface flows in a narrow channel. Phys. Fluids 19 (8), 088102.Google Scholar
Joseph, D. D. & Saut, J. C. 1990 Short-wave instabilities and ill-posed initial-value problems. Theor. Comput. Fluid Dyn. 1 (4), 191–227.Google Scholar
Kamrin, K. 2010 Nonlinear elasto-plastic model for dense granular flow. Intl J. Plast. 26 (2), 167–188.Google Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a 𝜇(I)-rheology. J. Fluid Mech. 686, 378–408.Google Scholar
Liu, A. J. & Nagel, S. R. 1998 Nonlinear dynamics: jamming is not just cool any more. Nature 396 (6706), 21–22.Google Scholar
Martin, N., Ionescu, I. R., Mangeney, A., Bouchut, F. & Farin, M. 2017 Continuum viscoplastic simulation of a granular column collapse on large slopes: 𝜇(I) rheology and lateral wall effects. Phys. Fluids 29 (1), 013301.Google Scholar
Midi, G. D. R. 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Morrison, J. A. 1956 Wave propagation in rods of Voigt material and visco-elastic materials with three-parameter models. Q. Appl. Maths 14 (2), 153–169.Google Scholar
Panton, R. 1968 The transient for Stokes’s oscillating plate: a solution in terms of tabulated functions. J. Fluid Mech. 31 (4), 819–825.Google Scholar
Preziosi, L. & Joseph, D. D. 1987 Stokes’ first problem for viscoelastic fluids. J. Non-Newtonian Fluid Mech. 25 (3), 239–259.Google Scholar
Pritchard, D., McArdle, C. R. & Wilson, S. K. 2011 The Stokes boundary layer for a power-law fluid. J. Non-Newtonian Fluid Mech. 166 (12), 745–753.Google Scholar
Savage, S. B. 1984 The mechanics of rapid granular flows. Adv. Appl. Mech. 24, 289–366.Google Scholar
Schlichting, H. 1968 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Staron, L., Lagrée, P.-Y. & Popinet, S. 2012 The granular silo as a continuum plastic flow: the hour-glass vs the clepsydra. Phys. Fluids 24 (10), 103301.Google Scholar
Stokes, G. G. 1851 On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Pitt Press.Google Scholar
Tanner, R. I. 1962 Note on the Rayleigh problem for a visco-elastic fluid. Z. Angew. Math. Phys. 13 (6), 573–580.Google Scholar
Thompson, P. A. & Grest, G. S. 1991 Granular flow: friction and the dilatancy transition. Phys. Rev. Lett. 67 (13), 1751.Google Scholar
Yakhot, V. & Colosqui, C. 2007 Stokes’ second flow problem in a high-frequency limit: application to nanomechanical resonators. J. Fluid Mech. 586, 249–258.Google Scholar