Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T11:37:54.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear wave evolution of shear-thinning Carreau liquid sheets

Published online by Cambridge University Press:  22 November 2018

Lujia Liu Open the ORCID record for Lujia Liu [Opens in a new window]  and
Lijun Yang
Lujia Liu
Affiliation:
School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijng 100191, PR China
Lijun Yang*
Affiliation:
School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijng 100191, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Researches on nonlinear instability of power-law plane sheets have been conducted using the Carreau model as the constitutive model. Combined with asymptotic expansion and long-wave assumption, the governing equations and boundary conditions were manipulated using integral transform. The first-order dimensionless dispersion relation between unstable growth rate and wavenumber was obtained and the second-order interface disturbance amplitude was calculated. By comparison and analysis of components of the second-order interface disturbance amplitude, it was found that the power-law index $n$ (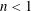$n<1$) only had an impact on instability of waves with the fundamental wavelength or one third the fundamental wavelength. The findings show that the Carreau-law rheological parameter 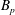$B_{p}$ has little impact on the second-order disturbance amplitude at the interfaces in a practical situation, while the Reynolds number has a positive effect on the growth rate of the disturbance amplitude for the power-law liquid sheets. Finally, the growth rates obtained by numerical simulation and analytical solution have been compared, and the results showed good agreement in the initial phase of wave evolution.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Instability: Nonlinear instability Non-Newtonian Flows: Non-Newtonian Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 659 - 676
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amaouche, M., Djema, A. & Abderrahmane, H. A. 2012 Film flow for power-law fluids: modeling and linear stability. Eur. J. Mech. (B/Fluids) 34, 70–84.Google Scholar
Balmforth, N. J., Craster, R. V. & Toniolo, C. 2003 Interfacial instability in non-Newtonian fluid layers. Phys. Fluids 15, 3370–3384.Google Scholar
Becerra, M. & Carvalho, M. S. 2011 Stability of viscoelastic liquid curtain. Chem. Engng Process. 50, 445–449.Google Scholar
Crapper, G. D., Dombrowski, N. & Jepson, W. P. 1975 Wave growth on thin sheets of non-Newtonian liquids. Proc. R. Soc. Lond. A 342, 225–236.Google Scholar
Goldin, M., Yerushalmi, J., Pfeffer, R. & Shinnar, R. 1969 Breakup of a laminar capillary jet of a viscoelastic fluid. J. Fluid Mech. 38, 689–711.Google Scholar
Gordon, M., Yerushalmi, J. & Shinnar, R. 1973 Instability of jets of non-Newtonian fluids. Trans. Soc. Rheol. 17, 303–324.Google Scholar
Jawadi, A., Boutyour, H. & Cadou, J. M. 2013 Asymptotic numerical method for steady flow of power-law fluids. J. Non-Newtonian Fluid Mech. 202, 22–31.Google Scholar
Kumar, S. 2001 Parametric instability of a liquid sheet. Proc. R. Soc. Lond. A 457, 1315–1326.Google Scholar
Lee, I. & Koo, J. 2010 Break-up characteristics of gelled propellant simulants with various gelling agent contents. Intl J. Therm. Sci. 19, 545–552.Google Scholar
Lee, J. C. & Rubin, H. 1975 On the breakup of molten polymeric threads. Rheol. Acta 14, 427–435.Google Scholar
Lin, J. S. & Hwang, C. C. 2000 Finite amplitude long-wave instability of power-law liquid films. Intl J. Non-Linear Mech. 35, 769–777.Google Scholar
Liu, L. J., Yang, L. J. & Ye, H. Y. 2016 Weakly nonlinear varicose-mode instability of planar liquid sheets. Phys. Fluids 28, 034105.Google Scholar
Liu, Z. B., Brenn, G. & Durst, F. 1998 Linear analysis of the instability of two-dimensional non-Newtonian liquid sheets. J. Non-Newtonian Fluid Mech. 78, 133–166.Google Scholar
Middleman, S. 1977 Fundamentals of polymer processing. In SERBIULA (sistema Librum 2.0). McGraw-Hill.Google Scholar
Paul, D. R. 1968 A study of spinnability in the wet-spinning of acrylic fibers. J. Appl. Polym. Sci. 12, 2273–2298.Google Scholar
Pearson, J. R. A. 1976 Instability in non-Newtonian flow. Annu. Rev. Fluid Mech. 8, 163–181.Google Scholar
Petrie, C. J. S. & Denn, M. M. 1976 Instabilities in polymer processing. AIChE J. 22, 209–236.Google Scholar
Ruyer-Quil, C., Chakraborty, S. & Dandapat, B. S. 2012 Wavy regime of a power-law film flow. J. Fluid Mech. 692, 220–256.Google Scholar
Tomar, G., Shankar, V., Shukla, S. K., Sharma, A. & Biswas, G. 2006 Instability and dynamics of thin viscoelastic liquid films. Eur. Phys. J. E 20, 185–200.Google Scholar
Yang, L. J., Tong, M. X. & Fu, Q. F. 2013 Instability of viscoelastic annular liquid sheets subjected to unrelaxed axial elastic tension. J. Non-Newtonian Fluid Mech. 198, 31–38.Google Scholar
Yang, L. J., Xu, B. R. & Fu, Q. F. 2012 Linear instability analysis of planar non-Newtonian liquid sheets in two gas streams of unequal velocities. J. Non-Newtonian Fluid Mech. 167–168, 50–58.Google Scholar
Yang, W. D. & Zhang, M. Z. 2005 Research and development of rheological and atomization characteristics of gelled propellants. J. Rocket Propulsion 31, 37–42.Google Scholar