Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Volino, Ralph J.
2020.
Turbulence structure in non-equilibrium boundary layers with favorable and adverse pressure gradients.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108717.
Romero, Sylvia
Zimmerman, Spencer
Philip, Jimmy
and
Klewicki, Joseph
2021.
Progress in Turbulence IX.
Vol. 267,
Issue. ,
p.
173.
HIKITA, Yudai
SUZUKI, Hiroki
KAMEDA, Takatsugu
and
MOCHIZUKI, Shinsuke
2021.
An experimental study on the equilibrium boundary layer subjected to favourable pressure gradient (Effect of pressure gradient on law of the wall).
Transactions of the JSME (in Japanese),
Vol. 87,
Issue. 894,
p.
20-00394.
Griffin, Kevin Patrick
Fu, Lin
and
Moin, Parviz
2021.
General method for determining the boundary layer thickness in nonequilibrium flows.
Physical Review Fluids,
Vol. 6,
Issue. 2,
Balin, Riccardo
and
Jansen, K.E.
2021.
Direct numerical simulation of a turbulent boundary layer over a bump with strong pressure gradients.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Mangavelli, Sai C.
Yuan, Junlin
and
Brereton, Giles J.
2021.
Effects of surface roughness topography in transient channel flows.
Journal of Turbulence,
Vol. 22,
Issue. 7,
p.
434.
Volino, Ralph J.
and
Schultz, Michael P.
2022.
Effects of boundary layer thickness on the estimation of equivalent sandgrain roughness in zero-pressure-gradient boundary layers.
Experiments in Fluids,
Vol. 63,
Issue. 8,
Pargal, Saurabh
Wu, Hao
Yuan, Junlin
and
Moreau, Stéphane
2022.
Adverse-pressure-gradient turbulent boundary layer on convex wall.
Physics of Fluids,
Vol. 34,
Issue. 3,
Romero, S.K.
Zimmerman, S.J.
Philip, J.
and
Klewicki, J.C.
2022.
Stress equation based scaling framework for adverse pressure gradient turbulent boundary layers.
International Journal of Heat and Fluid Flow,
Vol. 93,
Issue. ,
p.
108885.
Romero, Sylvia
Zimmerman, Spencer
Philip, Jimmy
White, Christopher
and
Klewicki, Joseph
2022.
Properties of the inertial sublayer in adverse pressure-gradient turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 937,
Issue. ,
Parthasarathy, Aadhy S.
and
Saxton-Fox, Theresa
2023.
Spectral analysis of a turbulent boundary layer encountering steady and unsteady complex pressure gradients.
Mangavelli, S. C.
and
Yuan, J.
2023.
Effects of form-induced velocity in rough-wall turbulent channel flows.
Journal of Turbulence,
Vol. 24,
Issue. 1-2,
p.
14.
Chen, Peng E.S.
Wu, Wen
Griffin, Kevin P.
Shi, Yipeng
and
Yang, Xiang I.A.
2023.
A universal velocity transformation for boundary layers with pressure gradients.
Journal of Fluid Mechanics,
Vol. 970,
Issue. ,
Volino, Ralph J.
and
Schultz, Michael P.
2023.
Comparison of smooth- and rough-wall non-equilibrium boundary layers with favourable and adverse pressure gradients.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Parthasarathy, Aadhy
and
Saxton-Fox, Theresa
2023.
A family of adverse pressure gradient turbulent boundary layers with upstream favourable pressure gradients.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Hansen, Christoffer
Yang, Xiang I.A.
and
Abkar, Mahdi
2023.
A POD-mode-augmented wall model and its applications to flows at non-equilibrium conditions.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Zaheer, Syed Qasim
and
Disimile, Peter J.
2023.
Simulation of SFS2 using Embedded LES: Part-II Understanding the asymmetry in bistable airwake at zero yaw.
Ocean Engineering,
Vol. 272,
Issue. ,
p.
113838.
Caiazzo, A.
Pargal, S.
Wu, H.
Sanjosé, M.
Yuan, J.
and
Moreau, S.
2023.
On the effect of adverse pressure gradients on wall-pressure statistics in a controlled-diffusion aerofoil turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
Deshpande, Rahul
van den Bogaard, Aron
Vinuesa, Ricardo
Lindić, Luka
and
Marusic, Ivan
2023.
Reynolds-number effects on the outer region of adverse-pressure-gradient turbulent boundary layers.
Physical Review Fluids,
Vol. 8,
Issue. 12,
Volino, Ralph J.
Fritsch, Daniel
Devenport, William J.
Eça, Luís
García-Mayoral, Ricardo
McKeon, Beverley
Piomelli, Ugo
Chung, Daniel
Vishwanathan, Vidya
Kerkvliet, Maarten
Toxopeus, Serge
and
Hutchins, Nicholas
2024.
Effects of roughness on non-equilibrium turbulent boundary layers.
Journal of Turbulence,
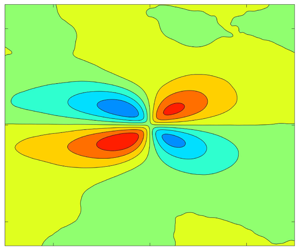
 $K$, was held constant. Two component velocity profiles were acquired at multiple streamwise locations to document the response to the changing pressure gradient of the mean velocity, Reynolds stresses and triple products of the fluctuating velocity components. Velocity field measurements were made to document the turbulence structure using two point correlations. In general, turbulence was suppressed by the FPG while structures became larger in streamwise and spanwise extent relative to the boundary layer thickness, particularly near the wall. In the recovery region, the return to canonical ZPG conditions was rapid. Changes in the structure in the APG region were less pronounced. The changes in the turbulence statistics and correlations relative to the ZPG baseline were quantified and presented as functions of streamwise location. When the streamwise location is scaled using the acceleration parameter, the results from all cases (including all statistical moments, and the size and inclination angles of turbulence structures), collapse in each region of the flow, showing a common non-equilibrium response to changes in the pressure gradient. These are new results which apply to the present flows and those with similar types of pressure gradients, but are not necessarily applicable to all flows with arbitrary pressure gradients.
$K$, was held constant. Two component velocity profiles were acquired at multiple streamwise locations to document the response to the changing pressure gradient of the mean velocity, Reynolds stresses and triple products of the fluctuating velocity components. Velocity field measurements were made to document the turbulence structure using two point correlations. In general, turbulence was suppressed by the FPG while structures became larger in streamwise and spanwise extent relative to the boundary layer thickness, particularly near the wall. In the recovery region, the return to canonical ZPG conditions was rapid. Changes in the structure in the APG region were less pronounced. The changes in the turbulence statistics and correlations relative to the ZPG baseline were quantified and presented as functions of streamwise location. When the streamwise location is scaled using the acceleration parameter, the results from all cases (including all statistical moments, and the size and inclination angles of turbulence structures), collapse in each region of the flow, showing a common non-equilibrium response to changes in the pressure gradient. These are new results which apply to the present flows and those with similar types of pressure gradients, but are not necessarily applicable to all flows with arbitrary pressure gradients.

