Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T14:53:46.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of an arbitrarily shaped particle in a density stratified fluid

Published online by Cambridge University Press:  13 March 2020

Rajat Dandekar ,
Vaseem A. Shaik  and
Arezoo M. Ardekani Open the ORCID record for Arezoo M. Ardekani [Opens in a new window]
Rajat Dandekar
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 49707, USA
Vaseem A. Shaik
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 49707, USA
Arezoo M. Ardekani*
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 49707, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

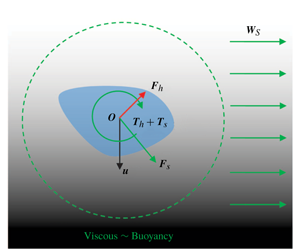
In this work, we theoretically investigate the motion of an arbitrarily shaped particle in a linear density stratified fluid with weak stratification and negligible inertia. We calculate the hydrodynamic force and torque experienced by the particle using the method of matched asymptotic expansions. We analyse our results for two classes of particles (non-skew and skew) depending on whether the particle possesses a centre of hydrodynamic stress. For both classes, we derive general expressions for the modified resistance tensors in the presence of stratification. We demonstrate the application of our results by considering some specific examples of particles settling in a direction parallel to the density gradient by considering both the limits of high ($Pe\gg 1$) and low ($Pe\ll 1$) Péclet numbers. We find that presence of stratification causes a slender body to rotate and settle along the broader side due to the contribution of the hydrostatic torque. Our work sheds light on the impact of stratification on the transport of arbitrarily shaped particles in density stratified environments in low-Reynolds-number regimes.

JFM classification

Geophysical and Geological Flows: Stratified flows Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A16
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ardekani, A. M., Doostmohammadi, A. & Desai, N. 2017 Transport of particles, drops, and small organisms in density stratified fluids. Phys. Rev. Fluids 2 (10), 100503.CrossRefGoogle Scholar
Ardekani, A. M. & Stocker, R. 2010 Stratlets: low Reynolds number point-force solutions in a stratified fluid. Phys. Rev. Lett. 105 (8), 084502.CrossRefGoogle Scholar
Bainbridge, R. 1957 The size, shape and density of marine phytoplankton concentrations. Biol. Rev. 32 (1), 91–115.CrossRefGoogle Scholar
Brenner, H. 1963 The Stokes resistance of an arbitrary particle. Chem. Engng Sci. 18 (1), 1–25.CrossRefGoogle Scholar
Brenner, H. 1964 The Stokes resistance of an arbitrary particle–II: an extension. Chem. Engng Sci. 19 (9), 599–629.CrossRefGoogle Scholar
Candelier, F., Mehaddi, R. & Vauquelin, O. 2014 The history force on a small particle in a linearly stratified fluid. J. Fluid Mech. 749, 184–200.CrossRefGoogle Scholar
Candelier, F., Mehlig, B. & Magnaudet, J. 2019 Time-dependent lift and drag on a rigid body in a viscous steady linear flow. J. Fluid Mech. 864, 554–595.CrossRefGoogle Scholar
Chadwick, R. S. & Zvirin, Y. 1974 Slow viscous flow of an incompressible stratified fluid past a sphere. J. Fluid Mech. 66 (2), 377–383.CrossRefGoogle Scholar
Childress, S. 1964 The slow motion of a sphere in a rotating, viscous fluid. J. Fluid Mech. 20 (2), 305–314.CrossRefGoogle Scholar
Childress, S. 1981 Mechanics of Swimming and Flying. Cambridge University Press.CrossRefGoogle Scholar
Cox, R. G. 1965 The steady motion of a particle of arbitrary shape at small Reynolds numbers. J. Fluid Mech. 23 (4), 625–643.CrossRefGoogle Scholar
Doostmohammadi, A. & Ardekani, A. M. 2014 Reorientation of elongated particles at density interfaces. Phys. Rev. 90 (3), 033013.Google ScholarPubMed
Doostmohammadi, A. & Ardekani, A. M. 2015 Suspension of solid particles in a density stratified fluid. Phys. Fluids 27 (2), 023302.CrossRefGoogle Scholar
Doostmohammadi, A., Dabiri, S. & Ardekani, A. M. 2014 A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J. Fluid Mech. 750, 5–32.CrossRefGoogle Scholar
Guasto, J. S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.CrossRefGoogle Scholar
Guidi, L., Chaffron, S., Bittner, L., Eveillard, D., Larhlimi, A., Roux, S., Darzi, Y., Audic, S., Berline, L., Brum, J. et al. 2016 Plankton networks driving carbon export in the oligotrophic ocean. Nature 532 (7600), 465–470.CrossRefGoogle ScholarPubMed
Happel, J. & Brenner, H. 1981 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, vol. 1. Springer.CrossRefGoogle Scholar
Harper, E. Y. & Chang, I. 1968 Maximum dissipation resulting from lift in a slow viscous shear flow. J. Fluid Mech. 33 (2), 209–225.CrossRefGoogle Scholar
Kellogg, W. W. 1980 Aerosols and climate. In Interactions of Energy and Climate, pp. 281–303. Springer.CrossRefGoogle Scholar
Kim, S. & Karrila, S. J. 2013 Microhydrodynamics: Principles and Selected Applications. Courier Corporation.Google Scholar
Kindler, K., Khalili, A. & Stocker, R. 2010 Diffusion-limited retention of porous particles at density interfaces. Proc. Natl Acad. Sci. USA 107 (51), 22163–22168.CrossRefGoogle ScholarPubMed
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12 (1), 435–476.CrossRefGoogle Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes, vol. 7. Cambridge University Press.CrossRefGoogle Scholar
Lofquist, K. E. & Purtell, L. P. 1984 Drag on a sphere moving horizontally through a stratified liquid. J. Fluid Mech. 148, 271–284.CrossRefGoogle Scholar
Mehaddi, R., Candelier, F. & Mehlig, B. 2018 Inertial drag on a sphere settling in a stratified fluid. J. Fluid Mech. 855, 1074–1087.CrossRefGoogle Scholar
Mercier, M. J., Wang, S., Péméja, J., Ern, P. & Ardekani, A. M. 2020 Settling disks in a linearly stratified fluid. J. Fluid Mech. 885, A2.CrossRefGoogle Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 The internal wave pattern produced by a sphere moving vertically in a density stratified liquid. J. Fluid Mech. 30 (3), 489–495.CrossRefGoogle Scholar
Mrokowska, M. M. 2018 Stratification-induced reorientation of disk settling through ambient density transition. Sci. Rep. 8 (1), 412.Google ScholarPubMed
Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.CrossRefGoogle Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.CrossRefGoogle Scholar
Turner, A. & Holmes, L. 2011 Occurrence, distribution and characteristics of beached plastic production pellets on the island of Malta (central Mediterranean). Mar. Pollut. Bull. 62 (2), 377–381.CrossRefGoogle Scholar
Warren, F. 1960 Wave resistance to vertical motion in a stratified fluid. J. Fluid Mech. 7 (2), 209–229.CrossRefGoogle Scholar
Yick, K. Y., Torres, C. R., Peacock, T. & Stocker, R. 2009 Enhanced drag of a sphere settling in a stratified fluid at small Reynolds numbers. J. Fluid Mech. 632, 49–68.CrossRefGoogle Scholar
Zvirin, Y. & Chadwick, R. S. 1975 Settling of an axially symmetric body in a viscous stratified fluid. Intl J. Multiphase Flow 1 (6), 743–752.CrossRefGoogle Scholar