Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T05:01:55.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Low-Reynolds-number flow past a cylinder with uniform blowing or sucking

Published online by Cambridge University Press:  09 September 2015

C. A. Klettner  and
I. Eames
C. A. Klettner*
Affiliation:
Department of Mechanical Engineering, University College London, Torrington Place, London WC1E 7JE, UK
I. Eames
Affiliation:
Department of Mechanical Engineering, University College London, Torrington Place, London WC1E 7JE, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the low-Reynolds-number flow generated by a cylinder (of radius $a$) in a stream (of velocity 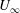$U_{\infty }$) which has a uniform through-surface blowing component (of velocity 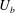$U_{b}$). The flow is characterized in terms of the Reynolds number 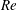$Re$ (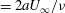$=2aU_{\infty }/{\it\nu}$, where ${\it\nu}$ is the kinematic viscosity of the fluid) and the dimensionless blow velocity 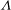${\it\Lambda}$ (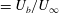$=U_{b}/U_{\infty }$). We seek the leading-order symmetric solution of the vorticity field which satisfies the near- and far-field boundary conditions. The drag coefficient is then determined from the vorticity field. For the no-blow case Lamb’s (Phil. Mag., vol. 21, 1911, pp. 112–121) expression is retrieved for $Re\rightarrow 0$. For the strong-sucking case, the asymptotic limit, 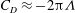$C_{D}\approx -2{\rm\pi}{\it\Lambda}$, is confirmed. The blowing solution is valid for 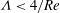${\it\Lambda}<4/Re$, after which the flow is unsymmetrical about 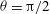${\it\theta}={\rm\pi}/2$. The analytical results are compared with full numerical solutions for the drag coefficient 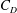$C_{D}$ and the fraction of drag due to viscous stresses. The predictions show good agreement for 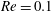$Re=0.1$ and 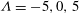${\it\Lambda}=-5,0,5$.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , R2
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics, 1st edn. Cambridge University Press.Google Scholar
Cliffe, K. A. & Lever, D. A. 1985 Isothermal flow past a blowing sphere. Intl J. Numer. Meth. Fluids 5, 709–725.CrossRefGoogle Scholar
Dennis, S. C. R. & Shimshoni, M. 1965 The steady flow of a viscous fluid past a circular cylinder. Ministry of Aviation – Aeronautical Research Council 797, 1–48.Google Scholar
Dukowicz, J. K. 1982 An exact solution for the drag of a sphere in low Reynolds number flow with strong uniform suction or blowing. Phys. Fluids 25, 1117–1118.CrossRefGoogle Scholar
Klettner, C. A. & Eames, I. 2012 The laminar free surface boundary layer of a solitary wave. J. Fluid Mech. 696, 423–433.CrossRefGoogle Scholar
Lamb, H. 1911 On the uniform motion of a sphere through a viscous fluid. Phil. Mag. 21, 112–121.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.CrossRefGoogle Scholar
Pankhurst, R. C. & Thwaites, B.1953 Experiments on the flow past a porous cylinder fitted with a Thwaites flap. Aero. Res. Council Reports and Memoranda. R. & M. 2787 (A.R.C. Technical Report). 29pp.Google Scholar
Stokes, G. G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Camb. Phil. Soc. 9, 8–106.Google Scholar
White, C. M. 1945 The drag of cylinders in fluids at low speeds. Proc. R. Soc. Lond. A 186, 472–479.Google Scholar
Zienkiewicz, O. C., Taylor, R. L. & Nithiarasu, P. 2005 The Finite Element Method for Fluid Dynamics, 6th edn. Butterworth-Heinemann.Google Scholar