Article contents
Invariant states in inclined layer convection. Part 1. Temporal transitions along dynamical connections between invariant states
Published online by Cambridge University Press: 08 July 2020
Abstract
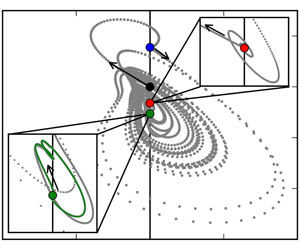
Thermal convection in an inclined layer between two parallel walls kept at different fixed temperatures is studied for fixed Prandtl number  $\mathit{Pr}=1.07$. Depending on the angle of inclination and the imposed temperature difference, the flow exhibits a large variety of self-organized spatio-temporal convection patterns. Close to onset, these patterns have been explained in terms of linear stability analysis of primary and secondary flow states. At a larger temperature difference, far beyond onset, experiments and simulations show complex, dynamically evolving patterns that are not described by stability analysis and remain to be explained. Here we employ a dynamical systems approach. We construct stable and unstable exact invariant states, including equilibria and periodic orbits of the fully nonlinear three-dimensional Oberbeck–Boussinesq equations. These invariant states underlie the observed convection patterns beyond their onset. We identify state space trajectories that, starting from the unstable laminar flow, follow a sequence of dynamical connections between unstable invariant states until the dynamics approaches a stable attractor. Together, the network of dynamically connected invariant states mediates temporal transitions between coexisting invariant states and thereby supports the observed complex time-dependent dynamics in inclined layer convection.
$\mathit{Pr}=1.07$. Depending on the angle of inclination and the imposed temperature difference, the flow exhibits a large variety of self-organized spatio-temporal convection patterns. Close to onset, these patterns have been explained in terms of linear stability analysis of primary and secondary flow states. At a larger temperature difference, far beyond onset, experiments and simulations show complex, dynamically evolving patterns that are not described by stability analysis and remain to be explained. Here we employ a dynamical systems approach. We construct stable and unstable exact invariant states, including equilibria and periodic orbits of the fully nonlinear three-dimensional Oberbeck–Boussinesq equations. These invariant states underlie the observed convection patterns beyond their onset. We identify state space trajectories that, starting from the unstable laminar flow, follow a sequence of dynamical connections between unstable invariant states until the dynamics approaches a stable attractor. Together, the network of dynamically connected invariant states mediates temporal transitions between coexisting invariant states and thereby supports the observed complex time-dependent dynamics in inclined layer convection.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 11
- Cited by


