Article contents
Impact of centrifugal buoyancy on strato-rotational instability
Published online by Cambridge University Press: 11 March 2020
Abstract
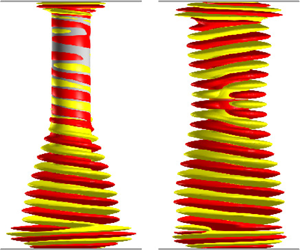
In a recent experiment on the flow between two concentric cylinders with the inner cylinder rotating and the fluid being stably stratified, Flór et al. (Phys. Fluids, vol. 30, 2018, 084103) found helical wave structures confined to the inner cylinder in an annulus with small inner-to-outer radius ratio (very large gap) in regimes where the Froude number (ratio of cylinder rotation frequency to buoyancy frequency) is less than one. These helical waves were reported to originate at the corners where the inner cylinder meets the top and bottom boundaries, and were found to be asymmetric with the lower helical wave being more intense. These observations are in marked contrast with other stratified Taylor–Couette experiments that employed much larger inner-to-outer radius ratios and much larger annulus height-to-gap ratios. Here, we present direct numerical simulations of the Navier–Stokes equations, with a Boussinesq approximation that accounts for centrifugal buoyancy effects which are normally neglected. Fixing the stratification and increasing the rotation rate of the inner cylinder (quantified by a Reynolds number), we find a sequence of bifurcations, each one introducing a new frequency, from the steady base state to a three-torus state. The instabilities are generated at the corners where the inner cylinder meets the endwalls, and the first instability is localized at the lower corner as a consequence of centrifugal buoyancy effects. We have also conducted simulations without centrifugal buoyancy and find that centrifugal buoyancy plays a crucial role in breaking the up–down reflection symmetry of the problem, capturing the most salient features of the experimental observations.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
Lopez and Marques supplementary movie 1
Animations of the two rotating waves found neglecting centrifugal buoyancy: the centrosymmetric rotating wave at Re=6150 and the reflection symmetric rotating wave at Re=6250.
Lopez and Marques supplementary movie 2
Animation of the rotating wave accounting for centrifugal buoyancy, at Re=6100.
- 9
- Cited by


