Published online by Cambridge University Press: 02 May 2023
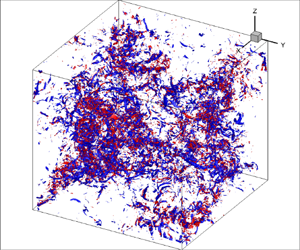
The Hall–Vinen–Bekharevich–Khalatnikov (HVBK) model is widely used to numerically study quantum turbulence in superfluid helium. Based on the two-fluid model of Tisza and Landau, the HVBK model describes the normal (viscous) and superfluid (inviscid) components of the flow using two Navier–Stokes type of equations, coupled through a mutual friction force term. We derive transport equations for the third-order moments for each component of velocity involving the fourth-order moments, which are classical probes for internal intermittency at any scale, and revealing the probability of rare and strong fluctuations. Budget equations are assessed through direct numerical simulations of the HVBK flow. We simulate a forced homogeneous isotropic turbulent flow with Reynolds number of the normal fluid (based on Taylor's microscale) close to 100. Values from 0.1 to 10 are considered for the ratio between the normal and superfluid densities. For these flows, an inertial range is not discernible and the restricted scaling range approach is used to take into account the finite Reynolds number (FRN) effect. We analyse the importance of each term in budget equations and emphasize their role in energy exchange between normal and superfluid components. Some interesting features are observed: (i) transport and pressure-related terms are dominant, similarly to single-fluid turbulence; and (ii) the mathematical signature of the FRN effect is weak despite the low value of the Reynolds number. The flatness of the velocity derivatives is finally studied through the transport equations and their limit for very small scales, and it is shown to gradually increase for lower and lower temperatures, for both normal fluid and superfluid. This similarity highlights the strong locking of the two fluids. The flatness factors are also found in reasonable agreement with classical turbulence.