Article contents
Heterogeneous dispersions as microcontinuum fluids
Published online by Cambridge University Press: 11 February 2020
Abstract
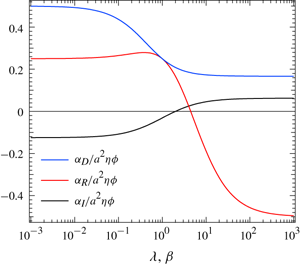
We present a non-local ‘microcontinuum’ constitutive equation describing particle suspensions undergoing heterogeneous flows in the low Stokes and particle Reynolds number regime. Most prior models rely on mesoscale averages of structural dynamics that smear out non-local effects or otherwise place strong restrictions on flow type. We relieve this restriction here by ensemble averaging the exact equations that govern the suspension at the microscale, thereby obtaining explicit structure-property connections. The result is a pointwise, heterogeneous ensemble average of the suspension stress valid for suspended particles of arbitrary shape, size, composition and concentration, as well as arbitrary sources of heterogeneity, including non-uniform shear fields, heterogeneous force fields or spatially varying volume fractions. This non-local model accounts for spatial and temporal variations in the flow structure over arbitrary length and time scales. We express the microcontinuum constitutive equation as a superposition of gradient operators that automatically accounts for flow heterogeneity over any length scale larger than the particle size. Batchelor’s result for a homogeneous suspension is recovered in the limit of zero gradients; non-zero gradient terms provide non-local corrections to the average stress and account for statistical heterogeneity in the suspension. We utilize energy methods to compute the influence of these gradient operators on the pointwise-averaged stress tensor, revealing a deep connection to the microhydrodynamics formalism. We apply this general framework to a dilute suspension of spherical particles and show that the resultant constitutive equations are consistent with experimental observations.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 2
- Cited by


