Article contents
Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders
Published online by Cambridge University Press: 05 January 2014
Abstract
The stability of the vertical path of a gravity- or buoyancy-driven disk of arbitrary thickness falling or rising in a viscous fluid, recently studied through direct numerical simulation by Auguste, Magnaudet & Fabre (J. Fluid Mech., vol. 719, 2013, pp. 388–405), is investigated numerically in the framework of global linear stability. The disk is allowed to translate and rotate arbitrarily and the stability analysis is carried out on the fully coupled system obtained by linearizing the Navier–Stokes equations for the fluid and Newton’s equations for the body. Three disks with different diameter-to-thickness ratios are considered: one is assumed to be infinitely thin, the other two are selected as archetypes of thin and thick cylindrical bodies, respectively. The analysis spans the whole range of body-to-fluid inertia ratios and considers Reynolds numbers (based on the fall/rise velocity and body diameter) up to 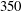 $350$. It reveals that four unstable modes with an azimuthal wavenumber
$350$. It reveals that four unstable modes with an azimuthal wavenumber  $m=\pm 1$ exist in each case. Three of these modes result from a Hopf bifurcation while the fourth is associated with a stationary bifurcation. Varying the body-to-fluid inertia ratio yields rich and complex stability diagrams with several branch crossings resulting in frequency jumps; destabilization/restabilization sequences are also found to take place in some subdomains. The spatial structure of the unstable modes is also examined. Analyzing differences between their real and imaginary parts (which virtually correspond to two different instants of time in the dynamics of a given mode) allows us to assess qualitatively the strength of the mutual coupling between the body and fluid. Qualitative and quantitative differences between present predictions and known results for wake instability past a fixed disk enlighten the fact that the first non-vertical regimes generally result from an intrinsic coupling between the body and fluid and not merely from the instability of the sole wake.
$m=\pm 1$ exist in each case. Three of these modes result from a Hopf bifurcation while the fourth is associated with a stationary bifurcation. Varying the body-to-fluid inertia ratio yields rich and complex stability diagrams with several branch crossings resulting in frequency jumps; destabilization/restabilization sequences are also found to take place in some subdomains. The spatial structure of the unstable modes is also examined. Analyzing differences between their real and imaginary parts (which virtually correspond to two different instants of time in the dynamics of a given mode) allows us to assess qualitatively the strength of the mutual coupling between the body and fluid. Qualitative and quantitative differences between present predictions and known results for wake instability past a fixed disk enlighten the fact that the first non-vertical regimes generally result from an intrinsic coupling between the body and fluid and not merely from the instability of the sole wake.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 44
- Cited by


