Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T06:43:04.596Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation regimes of vortex rings in negatively buoyant starting jets

Published online by Cambridge University Press:  25 January 2013

C. Marugán-Cruz ,
J. Rodríguez-Rodríguez  and
C. Martínez-Bazán
C. Marugán-Cruz
Affiliation:
Departamento de Ingeniería Térmica y de Fluidos, Universidad Carlos III de Madrid, 28911 Leganés, Spain
J. Rodríguez-Rodríguez*
Affiliation:
Departamento de Ingeniería Térmica y de Fluidos, Universidad Carlos III de Madrid, 28911 Leganés, Spain
C. Martínez-Bazán
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Mecánica y Minera, Universidad de Jaén, Campus de Las Lagunillas, 23071 Jaén, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The formation of vortex rings in negatively buoyant starting jets has been studied numerically for different values of the Richardson number, $\mathit{Ri}$, covering the range of weak to moderate buoyancy effects (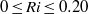$0\leq \mathit{Ri}\leq 0. 20$). Two different regimes have been identified in the vortex formation and the transition between them takes place at 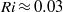$\mathit{Ri}\approx 0. 03$. The vorticity distribution inside the vortex ring after pinching off from the trailing stem as well as the total amount of circulation it encloses (characterized by the formation number, 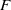$F$) show different behaviours with the Richardson number in the two regimes. The differences are associated with the different mechanisms by which the head vortex absorbs the circulation injected by the starting jet. While secondary vortices are engulfed by the leading vortex before separating from the trailing jet in the weak buoyancy effects regime (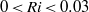$0\lt \mathit{Ri}\lt 0. 03$), this phenomenon is not observed in the moderate buoyancy effects regime (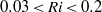$0. 03\lt \mathit{Ri}\lt 0. 2$). Moreover it is shown that the formation number of a negatively buoyant vortex ring can be determined by considering that its dynamics are similar to that of a neutrally buoyant vortex but propagating with velocity corresponding to the negatively buoyant one. Based on this simple idea, a phenomenological model is presented to describe quantitatively the evolution of the formation number with the Richardson number, $F(\mathit{Ri})$, obtained numerically. In addition, the limitations of different vortex identification methods used to evaluate the vortex properties in buoyant flows are discussed.

JFM classification

Convection: Plumes/thermals Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 470 - 486
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Didden, N. 1979 Formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30, 101–116.CrossRefGoogle Scholar
Fouras, A. & Soria, J. 1998 Accuracy of out-of-plane vorticity measurements derived from in-plane velocity field data. Exp. Fluids 25, 409–430.CrossRefGoogle Scholar
Gao, L. & Yu, S. C. M. 2010 A model for the pinch-off process of the leading vortex ring in a starting jet. J. Fluid Mech. 656, 205–222.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Iglesias, I., Vera, M., Sánchez, A. L. & Linán, A. 2005 Simulations of starting gas jets at low Mach numbers. Phys. Fluids 17, 038105.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Lin, W. & Armfield, S. W. 2000a Direct simulation of weak axisymmetric fountains in a homogeneous fluid. J. Fluid Mech. 403, 67–88.CrossRefGoogle Scholar
Lin, W. & Armfield, S. W. 2000b Very weak fountains in a homogeneous fluid. Numer. Heat Transfer A 38, 377–396.Google Scholar
Marugán-Cruz, C., Rodríguez-Rodríguez, J. & Martínez-Bazán, C. 2009 Negatively buoyant starting jets. Phys. Fluids 21, 117101.CrossRefGoogle Scholar
Myrtroeen, O. J. & Hunt, G. R. 2010 Negatively buoyant projectiles – from weak fountains to heavy vortices. J. Fluid Mech. 657, 227–237.CrossRefGoogle Scholar
Okubo, A. 1970 Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep-Sea Res. 17, 445–454.Google Scholar
Pawlak, G., Marugán-Cruz, C., Martínez-Bazán, C. & García-Hrdy, P. 2007 Experimental characterization of starting jet dynamics. Fluid Dyn. Res. 39, 711–730.CrossRefGoogle Scholar
Riley, N. 1998 The fascination of vortex rings. Appl. Sci. Res. 58, 169–189.CrossRefGoogle Scholar
Rosenfeld, M., Rambod, E. & Gharib, M. 1998 Circulation and formation of laminar vortex rings. J. Fluid Mech. 376, 297–318.CrossRefGoogle Scholar
Saffman, P. G. 1981 Dynamics of vorticity. J. Fluid Mech. 106, 49–58.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Schram, C. & Riethmuller, M. L. 2001 Vortex ring evolution in an impulsively started jet using digital particle image velocimetry and continuous wavelet analysis. Meas. Sci. Technol. 12, 1413–1421.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12, 618–621.CrossRefGoogle Scholar
Turner, J. S. 1957 Buoyant vortex rings. Proc. R. Soc. Lond. A 239, 61–75.Google Scholar
Wang, R. Q., Law, A. W. K. & Adams, E. E. 2011 Pinch-off and formation number of negatively buoyant jets. Phys. Fluids 23, 052101.CrossRefGoogle Scholar
Wang, R. Q., Law, A. W. K., Adams, E. E. & Fringer, O. B. 2009 Buoyant formation number of a starting buoyant jet. Phys. Fluids 21, 125104.CrossRefGoogle Scholar
Weast, R. C. 1985 CRC Handbook of Chemistry and Physics. CRC.Google Scholar
Weigand, A. & Gharib, M. 1997 On the evolution of laminar vortex rings. Exp. Fluids 22, 447–457.CrossRefGoogle Scholar
Weiss, J. 1991 The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48, 273–294.CrossRefGoogle Scholar

Marugán-Cruz et al. supplementary movie

Formation of the vortex corresponding to Ri=0.02

Download Marugán-Cruz et al. supplementary movie(Video)
Video 8.7 MB

Marugán-Cruz et al. supplementary movie

Formation of the vortex corresponding to Ri=0.025

Download Marugán-Cruz et al. supplementary movie(Video)
Video 7.4 MB

Marugán-Cruz et al. supplementary movie

Formation of the vortex corresponding to Ri=0.03

Download Marugán-Cruz et al. supplementary movie(Video)
Video 9.9 MB

Marugán-Cruz et al. supplementary movie

Formation of the vortex corresponding to Ri=0.04

Download Marugán-Cruz et al. supplementary movie(Video)
Video 9.7 MB