Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T09:07:13.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension to nonlinear stability theory of the circular Couette flow

Published online by Cambridge University Press:  19 April 2016

Pun Wong Yau ,
Shixiao Wang  and
Zvi Rusak
Pun Wong Yau
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland 1142, New Zealand
Shixiao Wang*
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland 1142, New Zealand
Zvi Rusak
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A nonlinear stability analysis of the viscous circular Couette flow to axisymmetric finite-amplitude perturbations under axial periodic boundary conditions is developed. The analysis is based on investigating the properties of a reduced Arnol’d energy-Casimir function 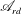$\mathscr{A}_{rd}$ of Wang (Phys. Fluids, vol. 2, 2009, 084104). A weighted kinetic energy of the perturbation, which has a form of 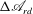${\rm\Delta}\mathscr{A}_{rd}$, the difference between the reduced Arnol’d function and its base flow value, is used as a Lyapunov function. We show that all the inviscid flow effects as well as all the viscous-dependent terms that are related to the flow boundaries vanish. The evolution of 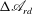${\rm\Delta}\mathscr{A}_{rd}$ depends only on the viscous effects of the perturbation’s dynamics inside the flow domain. The requirement for the temporal decay of 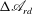${\rm\Delta}\mathscr{A}_{rd}$ leads to two novel sufficient conditions for the nonlinear stability of the circular Couette flow in response to axisymmetric perturbations. The linearized version of these conditions for infinitesimally small perturbations recovers the recent linear stability results by Kloosterziel (J. Fluid Mech., vol. 652, 2010, pp. 171–193). By examining the nonlinear stability conditions, we establish a definite operational region of the viscous circular Couette flow that is independent of the fluid viscosity. In this region of operation, the flow is nonlinearly stable in response to perturbations of any size, provided that the initial total circulation function is above a minimum level determined by the operational conditions of the base flow. Comparisons with historical studies show that our results shed light on the experimental measurements of Wendt (Ing.-Arch., vol. 4, 1933, pp. 577–595) and extend the classical nonlinear stability results of Serrin (Arch. Rat. Mech. Anal., vol. 3, 1959, pp. 1–13) and Joseph & Hung (Arch. Rat. Mech. Anal., vol. 44, 1971, pp. 1–22). When the flow is nonlinearly stable and evolves axisymmetrically for all time, then it always decays asymptotically in time to the circular Couette flow determined uniquely by the set-up of the rotating cylinders. Finally, we derive upper-bound estimates on the decay rate of finite-amplitude perturbations for the solid-body rotation flow between two coaxial rotating cylinders and for the circular Couette flow. We demonstrate via numerical simulations that the theoretical upper bound is relevant to the dynamics of various axisymmetric perturbations tested, where it is strictly obeyed. This present study provides new physical insights into a classical flow problem that was studied for many decades.

JFM classification

Geophysical and Geological Flows: Rotating flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 455 - 493
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abarbanel, H. D. I., Holm, D. D., Marsden, J. E. & Ratiu, T. S. 1986 Nonlinear stability analysis of stratified fluid equilibria. Phil. Trans. R. Soc. Lond. A 318, 349–409.Google Scholar
Adams, R. A. & Fournier, J. F. 2003 Sobolev Space, 2nd edn. Academic.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Arnol’d, V. I. 1965 Conditions for the nonlinear stability of the stationary plane curvilinear flows of an ideal fluid. Dokl. Akad. Nauk 162, 773–777.Google Scholar
Arnol’d, V. I. 1969 On an a priori estimate in the theory of hydrodynamic stability. Am. Math. Soc. Transl. 19, 267–269.Google Scholar
Arnol’d, V. I. & Khesin, B. A. 1998 Topological Methods in Hydrodynamics. (Applied Mathematical Science) , Springer.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (3), 385–425.Google Scholar
Couette, M. 1890 Études sur le Frottement des Liquides. Gauthier-Villars.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Joseph, D. D. & Hung, W. 1971 Contributions to the nonlinear theory of stability of viscous flow in pipes and between rotating cylinders. Arch. Rat. Mech. Anal. 44, 1–22.Google Scholar
Kelvin, L. 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007 Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.Google Scholar
Kloosterziel, R. C. 2010 Viscous symmetric stability of circular flows. J. Fluid Mech. 652, 171–193.CrossRefGoogle Scholar
Krueger, E. R., Gross, A. & Di Prima, R. C. 1966 On the relative importance of Taylor-vortex and non-axisymmetric modes in flow between rotating cylinders. J. Fluid Mech. 24, 521–538.Google Scholar
Rayleigh, L. 1916 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of near-critical swirling flows in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.CrossRefGoogle Scholar
Rusak, Z., Granata, J. & Wang, S. 2015 An active feedback flow control theory of the axisymmetric vortex breakdown process. J. Fluid Mech. 774, 488–528.CrossRefGoogle Scholar
Serrin, J. 1959 On the stability of viscous fluid motions. Arch. Rat. Mech. Anal. 3, 1–13.Google Scholar
Synge, J. L. 1933 The stability of heterogeneous liquids. Trans. R. Soc. Can. 27, 1–18.Google Scholar
Synge, J. L. 1938a Hydrodynamic stability. Semicentennial Publ. Math. Soc. 2, 269.Google Scholar
Synge, J. L. 1938b On the stability of a viscous liquid between two rotating coaxial cylinders. Proc. R. Soc. Akad. A 167, 250–256.Google Scholar
Szeri, A. & Holmes, P. 1988 Nonlinear stability of axisymmetric swirling flows. Phil. Trans. R. Soc. Lond. A 326, 327–354.Google Scholar
Taylor, G. L. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Vladimirov, V. A. 1986a Analogues of the Lagrange theorem in the hydrodynamics of whirling and stratified liquids. Z. Angew. Math. Mech. 50 (5), 559–564.CrossRefGoogle Scholar
Vladimirov, V. A. 1986b On nonlinear stability of incompressible fluid flows. Arch. Mech. 38 (5–6), 689–696.Google Scholar
Wang, S. 2009 On the nonlinear stability of inviscid axisymmetric swirling flows in a pipe of finite length. Phys. Fluids 21, 084104.CrossRefGoogle Scholar
Wendt, F. 1933 Turbulente Strömungen zwischen zwei rotierenden konaxialen Zylindern. Ing.-Arch. 4, 577–595.CrossRefGoogle Scholar
Wu, J. Z., Ma, H. Y. & Zhou, M. D. 2006 Vorticity and Vortex Dynamics. Springer.Google Scholar