Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T10:02:56.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Extended Squire’s transformation and its consequences for transient growth in a confined shear flow

Published online by Cambridge University Press:  13 March 2014

J. John Soundar Jerome  and
Jean-Marc Chomaz
J. John Soundar Jerome*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), École Polytechnique, 91128 Palaiseau, France
Jean-Marc Chomaz
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), École Polytechnique, 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The classical Squire transformation is extended to the entire eigenfunction structure of both Orr–Sommerfeld and Squire modes. For arbitrary Reynolds numbers 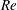$\mathit{Re}$, this transformation allows the solution of the initial-value problem for an arbitrary three-dimensional (3D) disturbance via a two-dimensional (2D) initial-value problem at a smaller Reynolds number 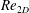$\mathit{Re}_{2D}$. Its implications for the transient growth of arbitrary 3D disturbances is studied. Using the Squire transformation, the general solution of the initial-value problem is shown to predict large-Reynolds-number scaling for the optimal gain at all optimization times $t$ with 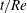${t}/{\mathit{Re}}$ finite or large. This result is an extension of the well-known scaling laws first obtained by Gustavsson (J. Fluid Mech., vol. 224, 1991, pp. 241–260) and Reddy & Henningson (J. Fluid Mech., vol. 252, 1993, pp. 209–238) for arbitrary 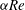$\alpha \mathit{Re}$, where $\alpha $ is the streamwise wavenumber. The Squire transformation is also extended to the adjoint problem and, hence, the adjoint Orr–Sommerfeld and Squire modes. It is, thus, demonstrated that the long-time optimal growth of 3D perturbations as given by the exponential growth (or decay) of the leading eigenmode times an extra gain representing its receptivity, may be decomposed as a product of the gains arising from purely 2D mechanisms and an analytical contribution representing 3D growth mechanisms equal to 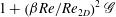$1+ \left (\beta \mathit{Re}/\mathit{Re}_{2D}\right )^2 \mathcal{G}$, where 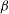$\beta $ is the spanwise wavenumber and 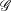$\mathcal{G}$ is a known expression. For example, when the leading eigenmode is an Orr–Sommerfeld mode, it is given by the product of respective gains from the 2D Orr mechanism and an analytical expression representing the 3D lift-up mechanism. Whereas if the leading eigenmode is a Squire mode, the extra gain is shown to be solely due to the 3D lift-up mechanism. Direct numerical solutions of the optimal gain for plane Poiseuille and plane Couette flow confirm the novel predictions of the Squire transformation extended to the initial-value problem. These results are also extended to confined shear flows in the presence of a temperature gradient.

JFM classification

Mathematical Foundations: General fluid mechanics Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 430 - 456
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayly, B. J., Orszag, S. A. & Herbert, T. 1988 Instability mechanisms in shear-flow transition. Annu. Rev. Fluid Mech. 20 (1), 359–391.Google Scholar
Boberg, L. & Brosa, U. 1988 Onset of turbulence in a pipe. Z. Naturforsch. 43 (8–9), 697–726.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
DiPrima, R. C. & Habetler, G. J. 1969 A completeness theorem for non-selfadjoint eigenvalue problem in hydrodynamic stability. Arch. Rat. Mech. Anal. 89, 211–228.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.Google Scholar
Farrell, B. F. 1988 Optimal excitation of perturbations in viscous shear flows. Phys. Fluids 31 (8), 2093–2102.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids A 5, 1390.Google Scholar
Gustavsson, L. 1991 Energy growth in three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.CrossRefGoogle Scholar
Gustavsson, L. H. & Hultgren, L. S. 1980 A resonant mechanism in plane Couette flow. J. Fluid Mech. 98, 149–159.Google Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20 (1), 487–526.Google Scholar
Herron, I. H. 1980 A completeness observation on the stability equations for stratified viscous shear flows. Phys. Fluids 23, 836–837.Google Scholar
Hultgren, L. S. & Gustavsson, L. H. 1981 Algebraic growth of disturbances in a laminar boundary layer. Phys. Fluids 24 (6), 1000–1004.Google Scholar
Jerome, J. J. S., Chomaz, J.-M. & Huerre, P. 2012 Transient growth in Rayleigh–Bénard-Poiseuille/Couette convection. Phys. Fluids 24 (4), 044103.Google Scholar
Joseph, D. D. 1976 Stability of Fluid Motions I. Springer.Google Scholar
Kachanov, Y. S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26 (1), 411–482.Google Scholar
Kendall, J. M. 1985 Experimental study of disturbances produced in a pre-transitional laminar boundary layer by weak freestream turbulence. AIAA Paper.Google Scholar
Klebanoff, P. S. 1971 Effects of free-stream turbulence on a laminar boundary layer. Bull. Am. Phys. Soc. 16.Google Scholar
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. 1962 The three-dimensional nature of boundary-layer instability. J. Fluid Mech. 12, 1–34.Google Scholar
Landhal, M. T. 1980 A note on the algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Lin, C. C. 1955 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Matsubara, M. & Alfredsson, P. H. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.Google Scholar
Moffatt, K. H. 1967 The interaction of turbulence with strong wind shear. In Proceedings of URSI-IUGG Colloquium on Atmospheric Turbulence and Radio Wave Propagatio (ed. Yaglom, A. M. & Tatarsk,  ), pp. 139–154. Nauka.Google Scholar
Morkovin, M. V.1968 Critical evaluation of transition from laminar to turbulent shear layer with emphasis on hypersonically traveling bodies. AFFDL Tech. Rep. pp. 68–149.Google Scholar
Morkovin, M. V.1978 Instability, transition to turbulence and predictability. AGARDograph No. 236, NATO Document.Google Scholar
Morkovin, M. V. 1984 Bypass transition to turbulence and research desiderata. Transit. Turbines 161–204.Google Scholar
Nicolas, X. 2002 Revue bibliographique sur les écoulements de Poiseuille-Rayleigh–Bénard: écoulements de convection mixte en conduites rectangulaires horizontales chauffées par le bas. Intl J. Therm. Sci. 41, 961–1016.Google Scholar
Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Proc. R. Irish Acad. A 27, 9–138.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.CrossRefGoogle Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34 (1), 291–319.CrossRefGoogle Scholar
Schensted, I. V.1961 Contributions to the theory of hydrodynamic stability. PhD thesis, University of Michigan, Ann Arbor, MI 48109, USA.Google Scholar
Schlichting, H. 1933 Zur entstehung der turbulenz bei der plattenströmung. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. 181–208.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory. MacGraw-Hill.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schubauer, G. B. & Skramstad, H. K. 1947 Laminar boundary-layer oscillations and stability of laminar flows. J. Aero. Sci. 14, 69–78.Google Scholar
Shanthini, R. 1989 Degeneracies of the temporal Orr–Sommerfeld eigenmodes in plane poiseuille flow. J. Fluid Mech. 201, 13–34.CrossRefGoogle Scholar
Squire, H. B. 1933 On the stability of 3D disturbances of viscous flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Tollmien, W. 1929 Über die entstehung der turbulenz. 1. Mitteilung. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. 21–44.Google Scholar
Vitoshkin, H., Heifetz, E., Gelfgat, A. Y. & Harnik, N. 2012 On the role of vortex stretching in energy optimal growth of three-dimensional perturbations on plane parallel shear flows. J. Fluid Mech. 707, 369–380.Google Scholar
Waleffe, F. 1995 Transition in shear flows. nonlinear normality versus non-normal linearity. Phys. Fluids 7, 3060.Google Scholar