Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T18:27:37.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental characterization of three-dimensional corner flows at low Reynolds numbers

Published online by Cambridge University Press:  19 July 2012

J. Sznitman ,
L. Guglielmini ,
D. Clifton ,
D. Scobee ,
H. A. Stone  and
A. J. Smits
J. Sznitman*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Department of Biomedical Engineering, Technion–Israel Institute of Technology, Haifa 32000, Israel
L. Guglielmini
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA
D. Clifton
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
D. Scobee
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
H. A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
A. J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate experimentally the characteristics of the flow field that develops at low Reynolds numbers (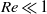) around a sharp 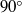corner bounded by channel walls. Two-dimensional planar velocity fields are obtained using particle image velocimetry (PIV) conducted in a towing tank filled with a silicone oil of high viscosity. We find that, in the vicinity of the corner, the steady-state flow patterns bear the signature of a three-dimensional secondary flow, characterized by counter-rotating pairs of streamwise vortical structures and identified by the presence of non-vanishing transverse velocities (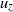). These results are compared to numerical solutions of the incompressible flow as well as to predictions obtained, for a similar geometry, from an asymptotic expansion solution (Guglielmini et al., J. Fluid Mech., vol. 668, 2011, pp. 33–57). Furthermore, we discuss the influence of both Reynolds number and aspect ratio of the channel cross-section on the resulting secondary flows. This work represents, to the best of our knowledge, the first experimental characterization of the three-dimensional flow features arising in a pressure-driven flow near a corner at low Reynolds number.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Stokesian dynamics Mathematical Foundations: General fluid mechanics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 37 - 52
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Balsa, T. F. 1998 Secondary flow in a Hele-Shaw cell. J. Fluid Mech. 372, 25–44.CrossRefGoogle Scholar
2. Gomilko, A. M., Malyuga, V. S. & Meleshko, V. V. 2003 On steady Stokes flow in a trihedral rectangular corner. J. Fluid Mech. 476, 159–177.CrossRefGoogle Scholar
3. Guglielmini, L., Rusconi, R., Lecuyer, S. & Stone, H. A. 2011 Three-dimensional features in low-Reynolds-number confined corner flows. J. Fluid Mech. 668, 33–57.CrossRefGoogle Scholar
4. Hills, C. P. & Moffatt, H. K. 2000 Rotary honings: a variant of the Taylor paint-scraper problem. J. Fluid Mech. 418, 119–135.CrossRefGoogle Scholar
5. Jeffrey, D. J. & Sherwood, J. D. 1980 Streamline patterns and eddies in low-Reynolds-number flow. J. Fluid Mech. 96, 315–334.CrossRefGoogle Scholar
6. Lauga, E., Stroock, A. D. & Stone, H. A. 2004 Three-dimensional flows in slowly varying planar geometries. Phys. Fluids 16, 3051–3062.CrossRefGoogle Scholar
7. Leong, C. W. & Ottino, J. M. 1989 Experiments on mixing due to chaotic advection in the cavity. J. Fluid Mech. 402, 463–469.CrossRefGoogle Scholar
8. Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.CrossRefGoogle Scholar
9. Moffatt, H. K. & Mak, V. 1998 Corner singularities in three-dimensional Stokes flow. In IUTAM Symposium on Non-linear Singularities in Deformation and Flow (ed. Durban, D. & Pearson, J. R. A. ), pp. 21–26. Kluwer.Google Scholar
10. Okamoto, K., Nishio, S., Saga, T. & Kobayashi, T. 2000 Standard images for particle-image velocimetry. Meas. Sci. Technol. 11, 685–691.CrossRefGoogle Scholar
11. Pan, F. & Acrivos, A. 1967 Steady flow in rectangular cavities. J. Fluid Mech. 28, 643–655.CrossRefGoogle Scholar
12. Riegels, F. 1938 Zur Kritik des Hele-Shaw Versuchs. Z. Angew. Math. Mech. 18, 95–106.CrossRefGoogle Scholar
13. Rusconi, R., Lecuyer, S., Guglielmini, L. & Stone, H. A. 2010 Laminar flow around corners triggers the formation of biofilm streamers. J. R. Soc. Interface 7, 1293–1299.CrossRefGoogle ScholarPubMed
14. Shankar, P. N. 1993 The eddy structure in Stokes flow in a cavity. J. Fluid Mech. 250, 371–383.CrossRefGoogle Scholar
15. Shankar, P. N. & Deshpande, M. D. 2000 Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136.CrossRefGoogle Scholar
16. Squires, T. M. & Quake, S. R. 2005 Microfluidics: fluid physics on the nanoliter scale. Rev. Mod. Phys. 77, 977–1026.CrossRefGoogle Scholar
17. Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics towards a lab-on-chip. Annu. Rev. Fluid Mech. 36, 381–411.CrossRefGoogle Scholar
18. Sveen, J. K. 2004 An introduction to matPIV v. 1.6.1. Tech. Rep., University of Oslo.Google Scholar
19. Taneda, S. 1979 Visualization of separating Stokes flow. J. Phys. Soc. Japan 46, 1935–1942.CrossRefGoogle Scholar
20. Thompson, B. W. 1968 Secondary flow in a Hele-Shaw cell. J. Fluid Mech. 31, 379–395.CrossRefGoogle Scholar
21. Yi, M. & Bau, H. H. 2003 The kinematics of bend-induced mixing in micro-conduits. Intl J. Heat Fluid Flow 24, 645–656.CrossRefGoogle Scholar