Article contents
The effect of magnetic field on perturbation evolution in homogeneously sheared flows
Published online by Cambridge University Press: 12 November 2018
Abstract
The goal of this paper is to identify and characterize the fundamental mechanisms that contribute toward flow stabilization in sheared plasma flows. Toward that end, we investigate the evolution of velocity and magnetic field perturbations in homogeneously sheared magnetohydrodynamic (MHD) flows subjected to an imposed streamwise magnetic field. The influences of magnetic field strength (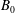 $B_{0}$) and perturbation wavevector orientation (
$B_{0}$) and perturbation wavevector orientation (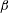 $\unicode[STIX]{x1D6FD}$) are characterized using linear analysis and direct numerical simulations. The linear analysis of ideal MHD indicates that the perturbation evolution is governed by four processes: pressure redistribution, kinetic energy production, kinetic–magnetic energy exchange and magnetic energy production due to magnetic stretching. The interplay between these processes can be characterized by the ratio of shear-to-magnetic timescales (
$\unicode[STIX]{x1D6FD}$) are characterized using linear analysis and direct numerical simulations. The linear analysis of ideal MHD indicates that the perturbation evolution is governed by four processes: pressure redistribution, kinetic energy production, kinetic–magnetic energy exchange and magnetic energy production due to magnetic stretching. The interplay between these processes can be characterized by the ratio of shear-to-magnetic timescales (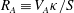 $R_{A}\equiv V_{A}\unicode[STIX]{x1D705}/S$) and
$R_{A}\equiv V_{A}\unicode[STIX]{x1D705}/S$) and 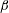 $\unicode[STIX]{x1D6FD}$, where
$\unicode[STIX]{x1D6FD}$, where 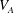 $V_{A}$,
$V_{A}$,  $\unicode[STIX]{x1D705}$ and
$\unicode[STIX]{x1D705}$ and 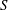 $S$ are Alfvén wave speed, initial wavenumber and mean flow shear, respectively. For cases with low values of
$S$ are Alfvén wave speed, initial wavenumber and mean flow shear, respectively. For cases with low values of 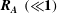 $\boldsymbol{R}_{\boldsymbol{A}}~(\ll \mathbf{1})$, a three-stage perturbation evolution is seen. At the first stage, pressure redistribution and production dominate leading to hydrodynamic-type behaviour. In the second stage, the onset of magnetic stretching process leads to an increase in magnetic energy. At late stages, production subsides and the dynamics is dominated by harmonic exchange between velocity and magnetic fields. For cases of
$\boldsymbol{R}_{\boldsymbol{A}}~(\ll \mathbf{1})$, a three-stage perturbation evolution is seen. At the first stage, pressure redistribution and production dominate leading to hydrodynamic-type behaviour. In the second stage, the onset of magnetic stretching process leads to an increase in magnetic energy. At late stages, production subsides and the dynamics is dominated by harmonic exchange between velocity and magnetic fields. For cases of 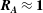 $\boldsymbol{R}_{\boldsymbol{A}}\approx \mathbf{1}$, the magnetic field reacts rapidly enough that hydrodynamic and magnetic production stages occur simultaneously followed by harmonic exchange. In the case of
$\boldsymbol{R}_{\boldsymbol{A}}\approx \mathbf{1}$, the magnetic field reacts rapidly enough that hydrodynamic and magnetic production stages occur simultaneously followed by harmonic exchange. In the case of 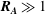 $\boldsymbol{R}_{\boldsymbol{A}}\gg 1$, all three stages occur simultaneously leading to harmonic exchange between kinetic and magnetic energies without any perturbation growth. For all cases considered, the late stage harmonic exchange results in equipartition between perturbation magnetic and kinetic energies. For a given
$\boldsymbol{R}_{\boldsymbol{A}}\gg 1$, all three stages occur simultaneously leading to harmonic exchange between kinetic and magnetic energies without any perturbation growth. For all cases considered, the late stage harmonic exchange results in equipartition between perturbation magnetic and kinetic energies. For a given 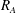 $R_{A}$, the effect of increasing
$R_{A}$, the effect of increasing 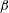 $\unicode[STIX]{x1D6FD}$ is to reduce the intensity of coupling and progressively slow down the three stages of evolution. For spanwise wavevector perturbations, the velocity–magnetic field interaction mechanism vanishes and there is no effect of pressure or magnetic field on individual velocity components.
$\unicode[STIX]{x1D6FD}$ is to reduce the intensity of coupling and progressively slow down the three stages of evolution. For spanwise wavevector perturbations, the velocity–magnetic field interaction mechanism vanishes and there is no effect of pressure or magnetic field on individual velocity components.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 3
- Cited by



