Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T00:30:12.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of inclination on the transition scenario in the wake of fixed disks and flat cylinders

Published online by Cambridge University Press:  30 March 2015

M. Chrust ,
C. Dauteuille ,
T. Bobinski ,
J. Rokicki ,
S. Goujon-Durand ,
J. E. Wesfreid ,
G. Bouchet  and
J. Dušek
M. Chrust*
Affiliation:
ICube, Department of Fluid Mechanics, Université de Strasbourg/CNRS, 2, rue Boussingault, 67000 Strasbourg, France
C. Dauteuille
Affiliation:
Ecole Polytechnique Féminine, 19, Boulevard Berthelot, 34000 Montpellier, France Institute of Aeronautics and Applied Mechanics, Warsaw University of Technology, Nowowiejska 24, 00-665 Warsaw, Poland
T. Bobinski
Affiliation:
Physique et Mécanique des Millieux Hétérogènes, PMMH, UMR 7636, ESPCI-CNRS-UPMC-UPD, 10, rue Vauquelin, 75231 Paris CEDEX 05, France Institute of Aeronautics and Applied Mechanics, Warsaw University of Technology, Nowowiejska 24, 00-665 Warsaw, Poland
J. Rokicki
Affiliation:
Institute of Aeronautics and Applied Mechanics, Warsaw University of Technology, Nowowiejska 24, 00-665 Warsaw, Poland
S. Goujon-Durand
Affiliation:
Physique et Mécanique des Millieux Hétérogènes, PMMH, UMR 7636, ESPCI-CNRS-UPMC-UPD, 10, rue Vauquelin, 75231 Paris CEDEX 05, France
J. E. Wesfreid
Affiliation:
Physique et Mécanique des Millieux Hétérogènes, PMMH, UMR 7636, ESPCI-CNRS-UPMC-UPD, 10, rue Vauquelin, 75231 Paris CEDEX 05, France
G. Bouchet
Affiliation:
Laboratoire IUSTI, Aix-Marseille Universite/CNRS, 5, rue Enrico Fermi, 13453 Marseille CEDEX 13, France
J. Dušek
Affiliation:
ICube, Department of Fluid Mechanics, Université de Strasbourg/CNRS, 2, rue Boussingault, 67000 Strasbourg, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We take up the old problem of Calvert (J. Fluid Mech., vol. 29, 1967, pp. 691–703) concerning the wake of a cylinder inclined with respect to the flow direction, and consider it from the viewpoint of transition to turbulence. For cylinders placed perpendicular to the flow direction, we address the disagreement between numerical simulation of the ideal axisymmetric configuration and experimental observations. We demonstrate that for a disk (a cylinder of aspect ratio infinity) and a flat cylinder of aspect ratio 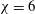${\it\chi}=6$ (ratio of diameter to height), the numerically predicted transition scenario is limited to very small inclination angles and is thus difficult to test experimentally. For inclination angles of about 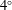$4^{\circ }$ and more, a joint numerical and experimental study shows that the experimentally observed scenario agrees qualitatively well with the results of numerical simulations. For the flat cylinder 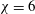${\it\chi}=6$, we obtain satisfactory agreement with regard to dependence of the critical Reynolds number (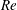$\mathit{Re}$) of the onset of vortex shedding on the inclination angle. Both for infinitely flat disks and cylinders of aspect ratio 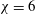${\it\chi}=6$, a small inclination tends to promote vortex shedding, that is, to lower the instability threshold, whereas for inclination angles exceeding 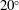$20^{\circ }$ the opposite effect is exhibited. The Strouhal number of oscillations is found to be only very weakly dependent on the Reynolds number, and very good agreement is obtained between values reported by Calvert (J. Fluid Mech., vol. 29, 1967, pp. 691–703) at high Reynolds numbers and our simulations at 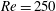$\mathit{Re}=250$. In contrast, we observe relatively poor agreement in Strouhal numbers when comparing the results of our numerical simulations and the data acquired from the experimental set-up described in this paper. Closer analysis shows that confidence can be placed in the numerical results because the discrepancy can be attributed to the influence of the support system of the flat cylinder. Suggestions for improvement of the experimental set-up are provided.

JFM classification

Instability: Instability Instability: Transition to turbulence Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , pp. 189 - 209
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auguste, F., Fabre, D. & Magnaudet, J. 2010 Bifurcations in the wake of thick circular disk. Theor. Comput. Fluid Dyn. 24, 305–313.CrossRefGoogle Scholar
Bobinski, T., Goujon-Durand, S. & Wesfreid, J. E. 2014 Instabilities in the wake of a circular disk. Phys. Rev. E 89, 053021.CrossRefGoogle ScholarPubMed
Bouchet, G., Mebarek, M. & Dušek, J. 2006 Hydrodynamic forces acting on a rigid fixed sphere in early transitional regimes. Eur. J. Mech. B 25, 321–336.CrossRefGoogle Scholar
Calvert, J. R. 1967 Experiments on the flow past an inclined disk. J. Fluid Mech. 29 (4), 691–703.CrossRefGoogle Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2010 Parametric study of the transition in the wake of oblate spheroids and flat cylinders. J. Fluid Mech. 665, 199–208.CrossRefGoogle Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25 (4), 044102.CrossRefGoogle Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2014 Effect of solid body degrees of freedom on the path instabilities of freely falling or rising flat cylinders. J. Fluids Struct. 47, 55–70.CrossRefGoogle Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.CrossRefGoogle Scholar
Ghidersa, B. & Dušek, J. 2000 Breaking of axisymmetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.CrossRefGoogle Scholar
Gumowski, K., Miedzik, J., Goujon-Durand, S., Jenffer, P. & Wesfreid, J. E. 2008 Transition to a time-dependent state of fluid flow in the wake of a sphere. Phys. Rev. E 77, 055308.CrossRefGoogle ScholarPubMed
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Klotz, L., Goujon-Durand, S., Rokicki, J. & Wesfreid, J. E. 2014 Experimental investigation of flow behind a cube for moderate Reynolds numbers. J. Fluid Mech. 750, 73–98.CrossRefGoogle Scholar
Meliga, P., Chomaz, J. M. & Sipp, D. 2009 Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.CrossRefGoogle Scholar
Shenoy, A. R. & Kleinstreuer, C. 2008 Flow over a thin circular disk at low to moderate Reynolds number. J. Fluid Mech. 605, 253–262.CrossRefGoogle Scholar
Szaltys, P., Chrust, M., Przadka, A., Goujon-Durand, S., Tuckerman, L. S. & Wesfreid, J. E. 2012 Nonlinear evolution of instabilities behind spheres and disks. J. Fluids Struct. 28, 483–487.CrossRefGoogle Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar