Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T11:37:30.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of expansion and collapse of explosive two-dimensional bubbles

Published online by Cambridge University Press:  22 November 2018

Jérôme Duplat Open the ORCID record for Jérôme Duplat [Opens in a new window]
Jérôme Duplat*
Affiliation:
Université Grenoble Alpes, INAC-SBT, Grenoble, F-38000, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An explosive gas mixture of hydrogen and oxygen is introduced in liquid water between two horizontal walls, forming a flat cylindrical bubble. Ignition and explosion of the bubble lead to a large depressurized cavity that finally implodes. We investigate the dynamics of the bubble collapse, which is qualitatively similar to the collapse of a spherical bubble. It exhibits a slightly weaker singularity than for spherical bubbles. We also analyse the explosion process. Starting with an initial radius 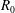$R_{0}$, the bubble reaches a maximal radius 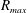$R_{max}$ that depends on the gap thickness 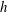$h$ between the two walls: for a thinner gap, the condensation of water vapour is more efficient, the overpressure consecutive to the combustion is weaker, and its duration is shorter. This leads to a smaller maximal radius 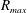$R_{max}$. An indirect measurement of the transport coefficient of hot water vapour can be inferred from this observation.

JFM classification

Drops and Bubbles: Bubble dynamics Phase change: Condensation/evaporation Phase change: Phase change
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 677 - 690
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blaik, M. & Christian, E. A. 1965 Near-surface measurements of deep explosions. Part I. Pressure pulses from small charges. J. Acoust. Soc. Am. 38 (1), 50–56.Google Scholar
Brenner, M. P., Hilgenfeldt, S. & Lohse, D. 2002 Single-bubble sonoluminescence. Rev. Mod. Phys. 74 (2), 425–484.Google Scholar
Chapman, N. R. 1988 Source levels of shallow explosive charges. J. Acoust. Soc. Am. 84 (2), 697–702.Google Scholar
Cole, R. H. 1948 Underwater Explosions. Princeton University Press.Google Scholar
Duplat, J. & Villermaux, E. 2015 Luminescence from collapsing centimeter bubbles expanded by chemical reaction. Phys. Rev. Lett. 115, 094501.Google Scholar
Flannigan, D. J. & Suslick, K. S. 2005 Plasma formation and temperature measurement during single-bubble cavitation. Nature 434 (7029), 52–55.Google Scholar
Hurricane, O. A. et al. 2014 Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 506, 343–348.Google Scholar
Landau, L. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
Lauterborn, W. 1974 Laser-induced cavitation. Acustica 31 (2), 51–78.Google Scholar
Li, J., Zhao, Z. W., Kazakov, A. & Dryer, F. L. 2004 An updated comprehensive kinetic model of hydrogen combustion. Intl J. Chem. Kinet. 36 (10), 566–575.Google Scholar
Lide, D. R.(Ed.) 2005 Handbook of Chemistry and Physics, 86th edn. CRC Press, Taylor & Francis.Google Scholar
Lindl, J. D. et al. 2011 Progress towards ignition on the national ignition facility. Nucl. Fusion 51, 094024.Google Scholar
Meyer, E. & Kuttruff, H. 1959 On the phase relation between sonoluminescence and the cavitation process with periodic excitation. Z. Angew. Phys. 11, 325–333.Google Scholar
Morley, C.2005 Gaseq: A Chemical Equilibrium Software for Windows (http://www.gaseq.co.uk).Google Scholar
Oguz, H. N. & Prosperetti, A. 1993 Dynamics of bubble growth and detachment from a needle. J. Fluid Mech. 257, 111–145.Google Scholar
Ohl, C. D., Lindau, O. & Lauterborn, W. 1998 Luminescence from spherically and aspherically collapsing laser induced bubbles. Phys. Rev. Lett. 80 (2), 393–396.Google Scholar
Plesset, M. S. & Prosperetti, A. 1977 Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 9, 145–185.Google Scholar
Rayleigh, Lord 1917 On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. 34 (200), 94–98.Google Scholar
Séon, T. & Antkowiak, A. 2012 Large bubble rupture sparks fast liquid jet. Phys. Rev. Lett. 109, 014501.Google Scholar
Storey, B. D. & Szeri, A. J. 2000 Water vapour, sonoluminescence and sonochemistry. Proc. R. Soc. Lond. A 456 (1999), 1685–1709.Google Scholar
Vledouts, A., Quinard, J., Vandenberghe, N. & Villermaux, E. 2016 Explosive fragmentation of liquid shells. J. Fluid Mech. 788, 246–273.Google Scholar
Walker, R. E. & Westenberg, A. A. 1960 Molecular diffusion studies in gases at high temperature. Part IV. Results and interpretation of the CO2 –O2 , CH4 –O2 , H2 –O2 , CO–O2 , and H2O–O2 systems. J. Chem. Phys. 32 (2), 436–442.Google Scholar
Zeldovich, Y. B. & Frank-Kamenetskii, D. A. 1938 On the theory of uniform flame propagation. Dokl. Akad. Nauk SSSR 19, 693–798.Google Scholar

Duplat supplementary movie 1

2D Bubble explosion and collapse (see figure 2)

Download Duplat supplementary movie 1(Video)
Video 2.7 MB

Duplat supplementary movie 2

Flame propagation after ignition

Download Duplat supplementary movie 2(Video)
Video 195.9 KB

Duplat supplementary movie 3

Expansion of a pure stoichiometric bubble with gap height h=0.92 mm, and initial radius $R_0$ = 2.1 mm. At maximal expansion, $R_{max}=3.1 mm$

Download Duplat supplementary movie 3(Video)
Video 1.1 MB

Duplat supplementary movie 4

Expansion of a bubble containing 50\% of inert gas, with similar characteristics of the bubble shown in movie 3: same gap height h=0.92 mm, and nearly same initial radius $R_0$ = 2 mm. Although this bubble contains less chemical energy it reaches a much larger maximal expansion ($R_{max}=3.9 mm ). As the inert gas do not condense they contribute significantly to the bubble expansion.

Download Duplat supplementary movie 4(Video)
Video 1.2 MB