Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wissink, J. G.
and
Herlina, H.
2016.
Direct numerical simulation of gas transfer across the air–water interface driven by buoyant convection.
Journal of Fluid Mechanics,
Vol. 787,
Issue. ,
p.
508.
Fredriksson, S. T.
Arneborg, L.
Nilsson, H.
and
Handler, R. A.
2016.
Surface shear stress dependence of gas transfer velocity parameterizations using DNS.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 10,
p.
7369.
Turney, D. E.
2016.
Coherent motions and time scales that control heat and mass transfer at wind-swept water surfaces.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 12,
p.
8731.
Herlina, H.
and
Wissink, J. G.
2016.
Isotropic-turbulence-induced mass transfer across a severely contaminated water surface.
Journal of Fluid Mechanics,
Vol. 797,
Issue. ,
p.
665.
Fredriksson, Sam T.
Arneborg, Lars
Nilsson, Håkan
Zhang, Qi
and
Handler, Robert A.
2016.
An evaluation of gas transfer velocity parameterizations during natural convection using DNS.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 2,
p.
1400.
Lacassagne, Tom
El-Hajem, Mahmoud
Morge, Fabien
Simoens, Serge
Champagne, Jean-Yves
and
Augier, F.
2017.
Study of Gas Liquid Mass Transfer in a Grid Stirred Tank.
Oil & Gas Science and Technology – Revue d’IFP Energies nouvelles,
Vol. 72,
Issue. 1,
p.
7.
Rodi, Wolfgang
2017.
Turbulence Modeling and Simulation in Hydraulics: A Historical Review.
Journal of Hydraulic Engineering,
Vol. 143,
Issue. 5,
Wissink, J. G.
Herlina, H.
Akar, Y.
and
Uhlmann, M.
2017.
Effect of surface contamination on interfacial mass transfer rate.
Journal of Fluid Mechanics,
Vol. 830,
Issue. ,
p.
5.
de Lamotte, Anne
Delafosse, Angélique
Calvo, Sébastien
Delvigne, Frank
and
Toye, Dominique
2017.
Investigating the effects of hydrodynamics and mixing on mass transfer through the free-surface in stirred tank bioreactors.
Chemical Engineering Science,
Vol. 172,
Issue. ,
p.
125.
Flores, Oscar
Riley, James J.
and
Horner-Devine, Alexander R.
2017.
On the dynamics of turbulence near a free surface.
Journal of Fluid Mechanics,
Vol. 821,
Issue. ,
p.
248.
Katul, Gabriel
Mammarella, Ivan
Grönholm, Tiia
and
Vesala, Timo
2018.
A Structure Function Model Recovers the Many Formulations for Air‐Water Gas Transfer Velocity.
Water Resources Research,
Vol. 54,
Issue. 9,
p.
5905.
Handler, Robert A.
and
Judd, K. Peter
2018.
Analysis of Infrared Radiation at an Air-Water Interface.
Frontiers in Mechanical Engineering,
Vol. 4,
Issue. ,
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
Lyon, A.
and
Champagne, J.-Y.
2019.
Oscillating grid turbulence in shear-thinning polymer solutions.
Physics of Fluids,
Vol. 31,
Issue. 8,
Herlina, H.
and
Wissink, J. G.
2019.
Simulation of air–water interfacial mass transfer driven by high-intensity isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
419.
Judd, K. Peter
and
Handler, Robert A.
2019.
Numerical Solution of the Radiation Transport Equation at an Air-Water Interface for a Stratified Medium.
Frontiers in Mechanical Engineering,
Vol. 5,
Issue. ,
Wissink, J. G.
and
Herlina, H.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
17.
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
and
Champagne, J.-Y.
2020.
Oscillating grid generating turbulence near gas-liquid interfaces in shear-thinning dilute polymer solutions.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Pinelli, Michele
Herlina, H.
Wissink, J.G.
and
Uhlmann, M.
2022.
Direct numerical simulation of turbulent mass transfer at the surface of an open channel flow.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Wissink, Jan G.
and
Herlina, H.
2023.
Surface-temperature-induced Marangoni effects on developing buoyancy-driven flow.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
Sanness Salmon, Henri R.
Baker, Lucia J.
Kozarek, Jessica L.
and
Coletti, Filippo
2023.
Effect of Shape and Size on the Transport of Floating Particles on the Free Surface in a Natural Stream.
Water Resources Research,
Vol. 59,
Issue. 10,
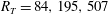 $R_T=84,195,507$). To allow a direct (unbiased) comparison of the instantaneous effects of scalar diffusivity, in each of the DNS up to six scalar advection–diffusion equations with different Schmidt numbers were solved simultaneously. As far as the authors are aware this is the first simulation that is capable to accurately resolve the realistic Schmidt number,
$R_T=84,195,507$). To allow a direct (unbiased) comparison of the instantaneous effects of scalar diffusivity, in each of the DNS up to six scalar advection–diffusion equations with different Schmidt numbers were solved simultaneously. As far as the authors are aware this is the first simulation that is capable to accurately resolve the realistic Schmidt number, 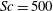 $\mathit{Sc}=500$, that is typical for the transport of atmospheric gases such as oxygen in water. For the range of turbulent Reynolds numbers and Schmidt numbers considered, the normalized transfer velocity
$\mathit{Sc}=500$, that is typical for the transport of atmospheric gases such as oxygen in water. For the range of turbulent Reynolds numbers and Schmidt numbers considered, the normalized transfer velocity 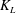 $K_L$ was found to scale with
$K_L$ was found to scale with 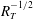 $R_T^{-{1/2}}$ and
$R_T^{-{1/2}}$ and 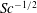 $\mathit{Sc}^{-{1/2}}$, which indicates that the largest eddies present in the isotropic turbulent flow introduced at the bottom of the computational domain tend to determine the mass transfer. The
$\mathit{Sc}^{-{1/2}}$, which indicates that the largest eddies present in the isotropic turbulent flow introduced at the bottom of the computational domain tend to determine the mass transfer. The 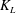 $K_L$ results were also found to be in good agreement with the surface divergence model of McCready, Vassiliadou & Hanratty (AIChE J., vol. 32, 1986, pp. 1108–1115) when using a constant of proportionality of 0.525. Although close to the surface large eddies are responsible for the bulk of the gas transfer, it was also observed that for higher
$K_L$ results were also found to be in good agreement with the surface divergence model of McCready, Vassiliadou & Hanratty (AIChE J., vol. 32, 1986, pp. 1108–1115) when using a constant of proportionality of 0.525. Although close to the surface large eddies are responsible for the bulk of the gas transfer, it was also observed that for higher 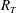 $R_T$ the influence of smaller eddies becomes more important.
$R_T$ the influence of smaller eddies becomes more important.

