Article contents
Deformation of a compliant wall in a turbulent channel flow
Published online by Cambridge University Press: 16 June 2017
Abstract
Interaction of a compliant wall with a turbulent channel flow is investigated experimentally by simultaneously measuring the time-resolved, three-dimensional (3D) flow field and the two-dimensional (2D) surface deformation. The optical set-up integrates tomographic particle image velocimetry to measure the flow with Mach–Zehnder interferometry to map the deformation. The Reynolds number is 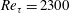 $Re_{\unicode[STIX]{x1D70F}}=2300$, and the Young’s modulus of the wall is 0.93 MPa, resulting in a ratio of shear speed to the centreline velocity (
$Re_{\unicode[STIX]{x1D70F}}=2300$, and the Young’s modulus of the wall is 0.93 MPa, resulting in a ratio of shear speed to the centreline velocity ( $U_{0}$) of 6.8. The wavenumber–frequency spectra of deformation show the surface motions consist of a non-advected low-frequency component and advected modes, some travelling downstream at approximately
$U_{0}$) of 6.8. The wavenumber–frequency spectra of deformation show the surface motions consist of a non-advected low-frequency component and advected modes, some travelling downstream at approximately 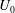 $U_{0}$ and others at
$U_{0}$ and others at 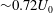 ${\sim}0.72U_{0}$. The r.m.s. values of the advected and non-advected modes are
${\sim}0.72U_{0}$. The r.m.s. values of the advected and non-advected modes are  $0.04~\unicode[STIX]{x03BC}\text{m}$
$0.04~\unicode[STIX]{x03BC}\text{m}$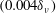 $(0.004\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}})$ and
$(0.004\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}})$ and 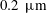 $0.2~\unicode[STIX]{x03BC}\text{m}$ (
$0.2~\unicode[STIX]{x03BC}\text{m}$ (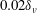 $0.02\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$), respectively, much smaller than the wall unit (
$0.02\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$), respectively, much smaller than the wall unit (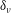 $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$), hence they do not affect the flow. Trends in the wall dynamics are elucidated by correlating the deformation with flow variables, including the 3D pressure distribution calculated by spatially integrating the material acceleration. Predictions by the Chase [J. Acoust. Soc. Am., vol. 89 (6), pp. 2589–2596] linear model are also calculated and compared to the measured trends. The spatial deformation–pressure correlations peak at
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$), hence they do not affect the flow. Trends in the wall dynamics are elucidated by correlating the deformation with flow variables, including the 3D pressure distribution calculated by spatially integrating the material acceleration. Predictions by the Chase [J. Acoust. Soc. Am., vol. 89 (6), pp. 2589–2596] linear model are also calculated and compared to the measured trends. The spatial deformation–pressure correlations peak at 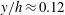 $y/h\approx 0.12$ (
$y/h\approx 0.12$ (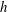 $h$ is half channel height), the elevation of Reynolds shear stress maximum in the log-layer. Streamwise lagging of the deformation behind the pressure is caused in part by phase lag of the pressure with decreasing distance from the wall, and in part by material damping. Positive deformations (bumps) caused by negative pressure fluctuations are preferentially associated with ejections involving spanwise vortices located downstream and quasi-streamwise vortices with spanwise offset. Results of conditional correlations are consistent with the presence of hairpin-like structures. The negative deformations (dimples) are preferentially associated with positive pressure fluctuations at the transition between an upstream sweep to a downstream ejection.
$h$ is half channel height), the elevation of Reynolds shear stress maximum in the log-layer. Streamwise lagging of the deformation behind the pressure is caused in part by phase lag of the pressure with decreasing distance from the wall, and in part by material damping. Positive deformations (bumps) caused by negative pressure fluctuations are preferentially associated with ejections involving spanwise vortices located downstream and quasi-streamwise vortices with spanwise offset. Results of conditional correlations are consistent with the presence of hairpin-like structures. The negative deformations (dimples) are preferentially associated with positive pressure fluctuations at the transition between an upstream sweep to a downstream ejection.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 37
- Cited by



