Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-20T12:36:08.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Decoupling ablation effects on boundary-layer stability and transition

Published online by Cambridge University Press:  20 November 2020

Fernando Miró Miró Open the ORCID record for Fernando Miró Miró [Opens in a new window]  and
Fabio Pinna Open the ORCID record for Fabio Pinna [Opens in a new window]
Fernando Miró Miró*
Affiliation:
Aeronautics and Aerospace Department, Von Karman Institute for Fluid Dynamics, Rhode-Saint-Genèse1640, Belgium
Fabio Pinna
Affiliation:
Aeronautics and Aerospace Department, Von Karman Institute for Fluid Dynamics, Rhode-Saint-Genèse1640, Belgium
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

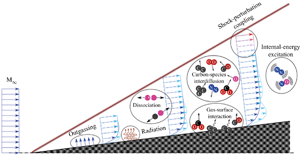
A modelling methodology is proposed and applied to effectively decouple many of the multiple physical phenomena simultaneously coexisting in boundary-layer-transition problems in the presence of an ablating thermal protection system. Investigations are based on linear stability theory and the semi-empirical $\textrm {e}^{\textrm {N}}$ method, and study the marginal contribution to second-mode-wave amplitudes of internal-energy-mode excitation, ablation-induced outgassing, ablation- and radiation-induced surface cooling, air- and carbon-species dissociation reactions, the interdiffusion of dissimilar species, surface chemistry and radiation and perturbation–shock interactions. The contributions of these phenomena are isolated by deploying a variety of flow assumptions, mixtures and boundary conditions with marginal increases in modelling complexity and generality. Internal-energy-mode excitation is seen to be the major contributor to the perturbation amplitudes for most conditions considered, whereas ablation-induced outgassing or the ablation- and radiation-induced modification of the surface-temperature distribution display a minor effect. Other phenomena are seen to have a variable contribution depending on the trajectory point, owing to the different ablation rates with which the thermal protection system decomposes. This is the case with the diffusion of carbon species injected through the surface, and the dissociation of air and carbon species. The use of a radiative equilibrium, rather than a homogeneous boundary condition on the temperature perturbation amplitude, is seen to increase the predicted growth of second-mode waves at all the trajectory points. Perturbation–shock interactions remarkably modify instability development only in scenarios with significant unstable supersonic modes. The substitution of all ablation subproducts for a single non-reacting species ($\textrm {CO}_{2}$) was acceptable as long as the flow chemistry can be assumed frozen. The use of inaccurate transport and diffusion models, rather than the state of the art, is seen to have a variable effect on the predictions, yet generally smaller than what was observed in previous work.

JFM classification

Boundary Layers: Boundary layer stability Compressible Flows: Compressible boundary layers Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 907 , 25 January 2021 , A14
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, J. D. Jr. 2006 Hypersonic and High Temperature Gas Dynamics, 2nd edn. American Institute of Aeronautics and Astronautics.Google Scholar
Aris, R. 1962 Vectors, Tensors, and the Basic Equations of Fluid Mechanics, 2nd edn. Dover, Prentice Hall.Google Scholar
Arnal, D. 1993 Boundary layer transition: predictions based on linear theory. In Special Course on Progress in Transition Modelling AGARD 793. AGARD.Google Scholar
Baker, R. L. 1977 Graphite sublimation chemistry nonequilibrium effects. AIAA J. 15 (10), 1391–1397.Google Scholar
Balakumar, P. 2013 Receptivity of hypersonic boundary layers to acoustic and vortical disturbances. AIAA Paper 2011-371.Google Scholar
Bellas-Chatzigeorgis, G., Turchi, A., Viladegut, A., Chazot, O., Barbante, P. & Magin, T. E. 2017 Development of catalytic and ablative gas–surface interaction models for the simulation of reacting gas mixtures. AIAA Paper 2017-4499.Google Scholar
Bellemans, A. & Magin, T. E. 2015 Calculation of collision integrals for ablation species. In 8th European Symposium on Aerothermodynamics for Space Vehicles, Lisbon, Portugal.Google Scholar
Berry, S. A., Nowak, R. J. & Horvath, T. J. 2004 Boundary layer control for hypersonic airbreathing vehicles. AIAA Paper 2004-2246.Google Scholar
Bertolotti, F. P. 1998 The influence of rotational and vibrational energy relaxation on boundary-layer stability. J. Fluid Mech. 372 (1998), 93–118.Google Scholar
Bertolotti, F. P., Herbert, T. & Spalart, P. R. 1992 Linear and nonlinear stability of the Blasius boundary layer. J. Fluid Mech. 242, 441–474.Google Scholar
Bitter, N. P. & Shepherd, J. E. 2015 Stability of highly cooled hypervelocity boundary layers. J. Fluid Mech. 778, 586–620.Google Scholar
Blottner, F. G., Johnson, M. & Ellis, M. 1971 Chemically reacting viscous flow program for multi-component gas mixtures. Tech. Rep. SC-RR-70-754. Sandia Laboratories.Google Scholar
Brazier, J. Ph., Aupoix, B. & Cousteix, J. 1991 Second-order effects in hypersonic laminar boundary layers. In Computational Methods in Hypersonic Aerodynamics (ed. T. K. S. Murthy). Kluwer Academic.Google Scholar
Brillouin, L. 1964 Tensors in Mechanics and Elasticity. Academic Press.Google Scholar
Chang, C.-L., Vinh, H. & Malik, M. R. 1997 Hypersonic boundary-layer stability with chemical reactions using PSE. AIAA Paper 1997-2012.Google Scholar
Chapman, S. & Cowling, T. G. 1939 The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction, and Diffusion in Gases. The University Press.Google Scholar
Choudhari, M. M., Li, F., Bynum, M., Kegerise, M. & King, R. A. 2015 Computations of disturbance amplification behind isolated roughness elements and comparison with measurements. AIAA Paper 2015-2625.Google Scholar
Choudhari, M. M., Li, F., Chang, C.-L., Edwards, J., Kegerise, M. & King, R. A. 2010 Laminar-turbulent transition behind discrete roughness elements in a high-speed boundary layer. AIAA Paper 2010-1575.Google Scholar
Clarey, M. P. & Greendyke, R. B. 2019 Thermochemical nonequilibrium processes in weakly ionized air using three-temperature models. J. Thermophys. Heat Transfer 33 (2), 425–440.Google Scholar
Elliott, O. S., Greendyke, R. B., Jewell, J. S. & Komives, J. R. 2019 Effect of carbon-based ablation products on hypersonic boundary layer stability. AIAA Scitech 2019 Forum 2019-0625.Google Scholar
Esfahanian, V. 1991 Computation and stability analysis of laminar flow over a blunt cone in hypersonic flow. PhD thesis, Ohio State University.Google Scholar
Eucken, A. 1913 Über das Wärmeleitvermögen, die spezifische Wärme und die innere Reibung der Gase (in german). Physik. Z. XIV, 324–332.Google Scholar
Fedorov, A. V. & Soudakov, V. G. 2014 Stability analysis of high-speed boundary-layer flow with gas injection. AIAA Paper 2014-2498.Google Scholar
Fertig, M., Dohr, A. & Frühauf, H.-H. 2001 Transport coefficients for high temperature nonequilibrium air flows. J. Thermophys. Heat Transfer 15 (2), 148–156.Google Scholar
Ferziger, J. H. & Kaper, H. G. 1972 Mathematical Theory of Transport Processes in Gases, 1st edn. North-Holland Publishing Company.Google Scholar
Fong, K. D., Wang, X., Huang, Y., Zhong, X., McKiernan, G. R., Fisher, R. A. & Schneider, S. P. 2015 Second mode suppression in hypersonic boundary layer by roughness: design and experiments. AIAA J. 53 (10), 3138–3143.Google Scholar
Franko, K. J., MacCormack, R. W. & Lele, S. K. 2010 Effects of chemistry modeling on hypersonic boundary layer linear stability prediction. AIAA Paper 2010-4601.Google Scholar
Fransson, J. H. M., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96 (6), 1–4.Google ScholarPubMed
Ghaffari, S., Marxen, O., Iaccarino, G. & Shaqfeh, E. S. G. 2010 Numerical simulations of hypersonic boundary-layer instability with wall blowing. AIAA Paper 2010-706.Google Scholar
Giovangigli, V. 1999 Multicomponent Flow Modeling. 3Island Press.Google Scholar
Groot, K. J., Miró Miró, F., Beyak, E. S., Moyes, A. J., Pinna, F. & Reed, H. L. 2018 DEKAF: spectral multi-regime basic-state solver for boundary layer stability. AIAA Paper 2018-3380.Google Scholar
Gupta, R. N., Yos, J. M., Thompson, R. A. & Lee, K.-P. 1990 A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30 000 K. Tech. Rep. RP-1232. National Aeronautics and Space Administration.Google Scholar
Gurvich, L., Veyts, I. & Alcock, C. 1989 Thermodynamic Properties of Individual Substances. Vol. 1, Elements O, H(D, T), F, Cl, Br, I, He, Ne, Ar, Kr, Xe, Rn, S, N, P and their Compounds. Part Two. Tables, 4th edn. Hemisphere Publishing Corporation.Google Scholar
Hannemann, K., Schramm, J. M. & Karl, S. 2008 Recent extensions to the high enthalpy shock tunnel Göttingen (HEG). In 2nd International ARA Days ‘Ten Years after ARD’, Arcachon, France.Google Scholar
Hein, S. J., Theiss, A., Di Giovanni, A., Stemmer, C., Schilden, T., Schröder, W., Paredes, P., Choudhari, M. M., Li, F. & Reshotko, E. 2019 Numerical investigation of roughness effects on transition on spherical capsules. J. Spacecr. Rockets 56 (2), 388–404.Google Scholar
Hermanns, M. & Hernández, J. A. 2008 Stable high-order finite-difference methods based on non-uniform grid point distributions. Intl J. Numer. Meth. Fluids 56, 233–255.Google Scholar
Hirschfelder, J. O., Curtiss, C. F. & Bird, R. B. 1954 Molecular theory of gases and liquids, 2nd edn. Wiley.Google Scholar
Hornung, H. G. 1992 Performance data of the new free-piston shock tunnel at GALCIT. In AIAA/ASME/SAE/ASEE 28th Joint Propulsion Conference and Exhibit, 1992, AIAA paper 92-3943.Google Scholar
Howe, J. T. 1989 Hypervelocity atmospheric flight: real gas flow fields. Tech. Rep. TM-101055. National Aeronautics and Space Administration.Google Scholar
Hudson, M. L., Chokani, N. & Candler, G. V. 1997 Linear stability of hypersonic flow in thermochemical nonequilibrium. AIAA J. 35 (6), 958–964.Google Scholar
van Ingen, J. L. 1956 A suggested semi-empirical method for the calculation of the boundary layer transition region. Tech. Rep. VTH-74. Technische Hogeschool Delft, Vliegtuigbouwkunde.Google Scholar
Itoh, K., Ueda, S., Komuro, T., Sato, K., Tanno, H. & Takahashi, M. 1999 Hypervelocity aerothermodynamic and propulsion research using a high enthalpy shock tunnel heist. In 9th International Space Planes and Hypersonic Systems and Technologies Conference, AIAA paper 99-499.Google Scholar
Iyer, P. S., Muppidi, S. & Mahesh, K. 2011 Roughness-induced transition in high speed flows. AIAA Paper 2011-566.Google Scholar
Johnson, C. B., Stainback, P. C., Wicker, K. C. & Boney, L. R. 1972 Boundary-layer edge conditions and transition Reynolds number data for a flight test at Mach 20 (Reentry F). Tech. Rep. TM X-2584. National Aeronautics and Space Administration, Washington D.C.Google Scholar
Johnson, H. B. & Candler, G. V. 2005 Hypersonic boundary layer stability analysis using PSE-Chem. AIAA Paper 2005-5023.Google Scholar
Johnson, H. B., Gronvall, J. E. & Candler, G. V. 2009 Reacting hypersonic boundary layer stability with blowing and suction. AIAA Paper 2009-938.Google Scholar
Kimmel, R. L., Adamczak, D., Paull, A., Paull, R., Shannon, J., Pietsch, R., Frost, M. & Alesi, H. 2015 HIFiRE-1 ascent-phase boundary-layer transition. J. Spacecr. Rockets 52 (1), 217–230.Google Scholar
Klentzman, J. & Tumin, A. 2013 Stability and receptivity of high speed boundary layers in oxygen. AIAA Paper 2013-2882.Google Scholar
Knisely, C. P. & Zhong, X. 2019 a Significant supersonic modes and the wall temperature effect in hypersonic boundary layers. AIAA J. 57 (4), 1552–1566.Google Scholar
Knisely, C. P. & Zhong, X. 2019 b Sound radiation by supersonic unstable modes in hypersonic blunt cone boundary layers. I. Linear stability theory. Phys. Fluids 31, 024103.Google Scholar
Knisely, C. P. & Zhong, X. 2019 c Sound radiation by supersonic unstable modes in hypersonic blunt cone boundary layers. II. Direct numerical simulation. Phys. Fluids 31, 024104.Google Scholar
Kuehl, J. J. 2018 Thermoacoustic interpretation of second-mode instability. AIAA J. 56 (9), 3585–3592.Google Scholar
Laub, B., Wright, M. J. & Venkatapathy, E. 2008 The Thermal Protection System (TPS) design and the relationship to atmospheric entry environments. In 6th International Planetary Probe Workshop.Google Scholar
Li, F., Choudhari, M. M., Chang, C.-L. & White, J. 2013 Effects of injection on the instability of boundary layers over hypersonic configurations. Phys. Fluids 25, 104107.Google Scholar
Lyttle, I. & Reed, H. L. 2005 Sensitivity of second-mode linear stability to constitutive models within hypersonic flow. AIAA Paper 2005-889.Google Scholar
Ma, Y. & Zhong, X. 2004 Receptivity to freestream disturbances of a mach 10 nonequilibrium reacting oxygen flow over a flat plate. AIAA Paper 2004-256.Google Scholar
Mack, L. M. 1984 Boundary-layer linear stability theory. In Special Course on Stability and Transition of Laminar Flow, AGARD 709. AGARD.Google Scholar
Magin, T. E. & Degrez, G. 2004 Transport algorithms for partially ionized and unmagnetized plasmas. J. Comput. Phys. 198 (2), 424–449.Google Scholar
Malik, M. R. 1989 a Prediction and control of transition in supersonic and hypersonic boundary layers. AIAA J. 27 (11), 1487–1493.Google Scholar
Malik, M. R. 1989 b Stability theory for chemically reacting flows. In Laminar-Turbulent Transition IUTAM Symposium (ed. D. Arnal & R. Michel). Toulouse, France.Google Scholar
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.Google Scholar
Malik, M. R. & Anderson, E. C. 1991 Real gas effects on hypersonic boundary-layer stability. Phys. Fluids 803 (3), 803–821.Google Scholar
Martin, N., Grossir, G., Miró Miró, F., Le Quang, D. & Chazot, O. 2019 Implementation of a laser-based Schlieren system for boundary layer instability investigation in the VKI H3 hypersonic wind tunnel. AIAA Paper 2019-0624.Google Scholar
Marxen, O., Magin, T. E., Shaqfeh, E. S. G. & Iaccarino, G. 2013 A method for the direct numerical simulation of hypersonic boundary-layer instability with finite-rate chemistry. J. Comput. Phys. 255, 572–589.Google Scholar
McBride, B. J., Zehe, M. J. & Gordon, S. 2002 NASA glenn coefficients for calculating thermodynamic properties of individual species. Tech. Rep. 2002-21155. National Aeronautics and Space Administration.Google Scholar
Milos, F. S. & Chen, Y. K. 2013 Ablation, thermal response, and chemistry program for analysis of thermal protection systems. J. Spacecr. Rockets 50 (1), 137–149.Google Scholar
Miró Miró, F. 2020 Numerical investigation of hypersonic boundary-layer stability and transition in the presence of ablation phenomena. PhD thesis, Université Libre de Bruxelles and von Karman Insitute for Fluid Dynamics.Google Scholar
Miró Miró, F., Beyak, E. S., Mullen, D., Pinna, F. & Reed, H. L. 2018 Ionization and dissociation effects on hypersonic boundary-layer stability. In 31st ICAS Congress. International Council of the Aeronautical Sciences.Google Scholar
Miró Miró, F., Beyak, E. S., Pinna, F. & Reed, H. L. 2019 a High-enthalpy models for boundary-layer stability and transition. Phys. Fluids 31, 044101.Google Scholar
Miró Miró, F., Dehairs, P., Pinna, F., Gkolia, M., Masutti, D., Regert, T. & Chazot, O. 2019 b Effect of wall blowing on hypersonic boundary-layer transition. AIAA J. 57 (4), 1567–1578.Google Scholar
Miró Miró, F. & Pinna, F. 2017 Linear stability analysis of a hypersonic boundary layer in equilibrium and non-equilibrium. AIAA Paper 2017-4518.Google Scholar
Miró Miró, F. & Pinna, F. 2018 Effect of uneven wall blowing on hypersonic boundary-layer stability and transition. Phys. Fluids 30, 084106.Google Scholar
Miró Miró, F. & Pinna, F. 2020 Injection-gas-composition effects on hypersonic boundary-layer transition. J. Fluid Mech. 890, R4.Google Scholar
Mortensen, C. 2018 Toward an understanding of supersonic modes in boundary-layer transition for hypersonic flow over blunt cones. J. Fluid Mech. 846, 789–814.Google Scholar
Mortensen, C. & Zhong, X. 2016 Real-gas and surface-ablation effects on hypersonic boundary-layer instability over a blunt cone. AIAA J. 54 (3), 980–998.Google Scholar
Paredes, P., Hermanns, M., Le Clainche, S. & Theofilis, V. 2013 Order $10^{4}$ speedup in global linear instability analysis using matrix formation. Comput. Meth. Appl. Mech. Engng 253, 287–304.Google Scholar
Park, C. 1976 Effects of atomic oxygen on graphite ablation. AIAA J. 14 (11), 1640–1642.Google Scholar
Pinna, F. 2013 VESTA toolkit: a software to compute transition and stability of boundary layers. AIAA Paper 2013-2616.Google Scholar
Pinna, F. & Groot, K. J. 2014 Automatic derivation of stability equations in arbitrary coordinates and different flow regimes. AIAA Paper 2014-2634.Google Scholar
Pinna, F., Miró Miró, F., Zanus, L., Padilla Montero, I. & Demange, S. 2019 Automatic derivation of stability equations and their application to hypersonic and high-enthalpy shear flows. In International Conference for Flight Vehicles, Aerothermodynamics and Re-entry Missions & Engineering, Monopoli, Italy.Google Scholar
Pinna, F. & Rambaud, P. 2013 Effects of shock on hypersonic boundary layer stability. Prog. Flight Phys. 5, 93–106.Google Scholar
Reed, H. L., Kimmel, R. L., Schneider, S. P. & Arnal, D. 1997 Drag prediction and transition in hypersonic flow. AIAA Paper 1997-1818.Google Scholar
Schneider, S. P. 2008 a Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.Google Scholar
Schneider, S. P. 2008 b Hypersonic boundary-layer transition experiments on blunt bodies with roughness. AIAA Paper 2008-501.Google Scholar
Schneider, S. P. 2010 Hypersonic boundary-layer transition with ablation and blowing. J. Spacecr. Rockets 47 (2), 225–237.Google Scholar
Schrooyen, P. 2015 Numerical simulation of aerothermal flows through ablative thermal protection systems. PhD thesis, UCL.Google Scholar
Scoggins, J. B. 2017 Development of numerical methods and study of coupled flow, radiation, and ablation phenomena for atmospheric entry. PhD thesis, Université Paris-Saclay and VKI.Google Scholar
Scoggins, J. B. & Magin, T. E. 2014 Development of mutation$++$: MUlticomponent thermodynamics and transport properties for IONized gases library in C$++$. AIAA Paper 2014-2966.Google Scholar
Shrestha, P. 2019 Numerical study of high-speed transition due to passive and active trips numerical study of high-speed transition due to passive and active trips. PhD thesis, University of Minnesota.Google Scholar
Shrestha, P. & Candler, G. V. 2019 Direct numerical simulation of high-speed transition due to roughness elements. J. Fluid Mech. 868, 762–788.Google Scholar
Smith, A. M. O. & Gamberoni, N. 1956 Transition, pressure gradient and stability theory. Tech. Rep. ES 26388. Douglas Aircraft Co., El Segundo, California.Google Scholar
Stuckert, G. & Reed, H. L. 1994 Linear disturbances in hypersonic, chemically reacting shock layers. AIAA J. 32 (7), 1384–1393.Google Scholar
Stuckert, G. K. 1991 Linear stability theory of hypersonic, chemically reacting viscous flows. PhD thesis, Arizona State University.Google Scholar
Sutherland, W. 1893 The viscosity of gases and molecular force. Phil. Mag. Ser. 5 36 (223), 507–531.Google Scholar
Tumin, A. 2008 Nonparallel flow effects on roughness-induced perturbations in boundary layers. J. Spacecr. Rockets 45 (6), 1176–1184.Google Scholar
Turchi, A., Congedo, P. M., Helber, B. & Magin, T. E. 2017 a Thermochemical ablation modeling forward uncertainty analysis—Part II: application to plasma wind-tunnel testing. Intl J. Therm. Sci. 118, 510–517.Google Scholar
Turchi, A., Congedo, P. M. & Magin, T. E. 2017 b Thermochemical ablation modeling forward uncertainty analysis—Part I: numerical methods and effect of model parameters. Intl J. Therm. Sci. 118, 497–509.Google Scholar
Vincenti, W. G. & Kruger, C. H. 1967 Introduction to Physical Gas Dynamics. Krieger.Google Scholar
Wagnild, R. M., Candler, G. V., Leyva, I. A., Jewell, J. S. & Hornung, H. G. 2010 Carbon dioxide injection for hypervelocity boundary layer stability. AIAA Paper 2010-1244.Google Scholar
Walker, S. H., Sherk, J., Shell, D., Schena, R., Bergmann, J. F. & Gladbach, J. 2008 The DARPA/AF Falcon program: the hypersonic technology vehicle #2 (HTV-2) flight demonstration Phase. In 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, AIAA paper 2008-2539.Google Scholar
Wartemann, V., Wagner, A., Wagnild, R. M., Pinna, F., Miró Miró, F., Tanno, H. & Johnson, H. B. 2018 High-enthalpy effects on hypersonic boundary-layer transition. J. Spacecr. Rockets 56 (2), 347–356.Google Scholar
Wheaton, B. M., Berridge, D. C., Wolf, T. D., Stevens, R. T. & McGrath, B. E. 2018 Boundary Layer Transition (BOLT) flight experiment overview. AIAA Paper 2018-2892.Google Scholar
White, F. M. 1991 Viscous Fluid Flow, 2nd edn. McGraw-Hill.Google Scholar
Wilke, C. R. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18 (4), 517–519.Google Scholar
Wright, M. J., Bose, D., Palmer, G. E. & Levin, E. 2005 Recommended collision integrals for transport property computations Part I: air species. AIAA J. 43 (12), 2558–2564.Google Scholar
Wright, M. J., Hwang, H. H. & Schwenke, D. W. 2007 Recommended collision integrals for transport property computations Part II: mars and venus entries. AIAA J. 45 (1), 281–288.Google Scholar
Wright, R. L. & Zoby, E. V. 1977 Flight boundary layer transition measurements on a slender cone at mach 20. AIAA Paper 77-719.Google Scholar
Zanus, L., Miró Miró, F. & Pinna, F. 2019 Weak non-parallel effects on chemically reacting hypersonic boundary layer stability. AIAA Paper 2019-2853.Google Scholar
Zanus, L., Miró Miró, F. & Pinna, F. 2020 Parabolized stability analysis of chemically reacting boundary layer flows in equilibrium conditions. Proc. Inst. Mech. Engrs 234 (1), 79–95.Google Scholar
Supplementary material: File

Miró Miró and Pinna supplementary material

Miró Miró and Pinna supplementary material

Download Miró Miró and Pinna supplementary material(File)
File 231.2 KB