Article contents
The controlled vertical impact of an inclined flat plate on a quiescent water surface
Published online by Cambridge University Press: 27 September 2019
Abstract
The generation of spray during the vertical impact of a flat plate (length 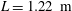 $L=1.22~\text{m}$, width
$L=1.22~\text{m}$, width 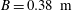 $B=0.38~\text{m}$) on a quiescent water surface is studied experimentally. The plate is held in an orientation tilted up from horizontal by angles
$B=0.38~\text{m}$) on a quiescent water surface is studied experimentally. The plate is held in an orientation tilted up from horizontal by angles 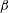 $\unicode[STIX]{x1D6FD}$ ranging from
$\unicode[STIX]{x1D6FD}$ ranging from 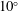 $10^{\circ }$ to
$10^{\circ }$ to 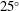 $25^{\circ }$ about one of its long edges, which is positioned close to a vertical wall. The plate motion, which is driven by a servo motor system, is set to maintain a constant speed,
$25^{\circ }$ about one of its long edges, which is positioned close to a vertical wall. The plate motion, which is driven by a servo motor system, is set to maintain a constant speed, 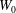 $W_{0}$, until the trailing (upper) long edge of the plate passes the still water level (SWL) and then to decelerate to a stop. The impact Froude numbers
$W_{0}$, until the trailing (upper) long edge of the plate passes the still water level (SWL) and then to decelerate to a stop. The impact Froude numbers 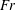 $\mathit{Fr}$ (
$\mathit{Fr}$ (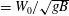 $=W_{0}/\sqrt{gB}$, where
$=W_{0}/\sqrt{gB}$, where 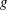 $g$ is the gravitational acceleration) range from 0.21 to 0.63. The evolution of the water surface underneath the plate and outboard of its trailing edge is measured with a cinematic laser induced fluorescence technique. As the plate’s leading (low) edge passes the SWL, the local water surface rises and develops into a thin spray sheet that travels along the plate’s lower surface toward the trailing edge. The horizontal speed of the under-plate spray tip is approximately
$g$ is the gravitational acceleration) range from 0.21 to 0.63. The evolution of the water surface underneath the plate and outboard of its trailing edge is measured with a cinematic laser induced fluorescence technique. As the plate’s leading (low) edge passes the SWL, the local water surface rises and develops into a thin spray sheet that travels along the plate’s lower surface toward the trailing edge. The horizontal speed of the under-plate spray tip is approximately 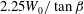 $2.25W_{0}/\tan \unicode[STIX]{x1D6FD}$, as high as
$2.25W_{0}/\tan \unicode[STIX]{x1D6FD}$, as high as 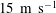 $15~\text{m}~\text{s}^{-1}$. In agreement with published similarity theory for the flow during the vertical water entry of a wedge, the under-plate surface profiles scaled by
$15~\text{m}~\text{s}^{-1}$. In agreement with published similarity theory for the flow during the vertical water entry of a wedge, the under-plate surface profiles scaled by 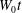 $W_{0}t$ nearly collapse on a single curve for each
$W_{0}t$ nearly collapse on a single curve for each 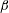 $\unicode[STIX]{x1D6FD}$. As the under-plate spray passes the plate’s trailing edge, it develops into the leading portion (called herein the Type I spray) of the outboard spray system. As the trailing edge of the plate passes through the local water surface, a crater develops and a large nearly vertical spray sheet (called the Type II spray) is generated from the outer edge (called the outboard spray root) of the crater. The characteristic horizontal length scale of the crater is found to expand in time following a power law with an exponent of approximately 0.77 for all conditions. A short time after its formation, the outboard spray root becomes the crest of a gravity wave whose propagation speed is of the order of
$\unicode[STIX]{x1D6FD}$. As the under-plate spray passes the plate’s trailing edge, it develops into the leading portion (called herein the Type I spray) of the outboard spray system. As the trailing edge of the plate passes through the local water surface, a crater develops and a large nearly vertical spray sheet (called the Type II spray) is generated from the outer edge (called the outboard spray root) of the crater. The characteristic horizontal length scale of the crater is found to expand in time following a power law with an exponent of approximately 0.77 for all conditions. A short time after its formation, the outboard spray root becomes the crest of a gravity wave whose propagation speed is of the order of 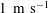 $1~\text{m}~\text{s}^{-1}$ for all
$1~\text{m}~\text{s}^{-1}$ for all 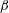 $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and 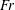 $\mathit{Fr}$. The dimensionless envelope of the Type II spray profiles collapse to a single curve at high
$\mathit{Fr}$. The dimensionless envelope of the Type II spray profiles collapse to a single curve at high 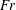 $\mathit{Fr}$ for each
$\mathit{Fr}$ for each 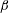 $\unicode[STIX]{x1D6FD}$. The connecting spray sheet between the Type I and Type II sprays tends to break up at small
$\unicode[STIX]{x1D6FD}$. The connecting spray sheet between the Type I and Type II sprays tends to break up at small 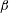 $\unicode[STIX]{x1D6FD}$ and large
$\unicode[STIX]{x1D6FD}$ and large 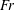 $\mathit{Fr}$.
$\mathit{Fr}$.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Wang and Duncan supplementary movie 1
LIF high-speed movie of the under-plate spray evolution for Fr = 0.53, β = 25° (corresponding to figure 5, figure 30).
Wang and Duncan supplementary movie 2
LIF high-speed movie of the outboard spray evolution for Fr = 0.53, β = 20° (corresponding to figure 13).
Wang and Duncan supplementary movie 3
LIF high-speed movie of the under-plate spray evolution for Fr = 0.21, β = 25°
Wang and Duncan supplementary movie 4
LIF high-speed movie of the outboard spray evolution for Fr = 0.53, β = 25° (corresponding to figure 30)
Wang and Duncan supplementary movie 5
LIF high-speed movies of the outboard spray evolution for four values of deadrise angles, β = 10°, 15°, 20° and 25°, all at the same Froude number, Fr = 0.53 (corresponding to figure 34).
- 6
- Cited by



