Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T11:43:50.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of amplifier flows using subspace identification techniques

Published online by Cambridge University Press:  17 May 2013

Fabien Juillet ,
Peter J. Schmid  and
Patrick Huerre
Fabien Juillet*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), CNRS Ecole Polytechnique, 91128 Palaiseau, France
Peter J. Schmid
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), CNRS Ecole Polytechnique, 91128 Palaiseau, France
Patrick Huerre
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), CNRS Ecole Polytechnique, 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A realistic, efficient and robust technique for the control of amplifier flows has been investigated. Since this type of fluid system is extremely sensitive to upstream environmental noise, an accurate model capturing the influence of these perturbations is needed. A subspace identification algorithm is not only a convenient and effective way of constructing this model, it is also realistic in the sense that it is based on input and output data measurements only and does not require other information from the detailed dynamics of the fluid system. This data-based control design has been tested on an amplifier model derived from the Ginzburg–Landau equation, and no significant loss of efficiency has been observed when using the identified instead of the exact model. Even though system identification leads to a realistic control design, other issues such as state estimation, have to be addressed to achieve full control efficiency. In particular, placing a sensor too far downstream is detrimental, since it does not provide an estimate of incoming perturbations. This has been made clear and quantitative by considering the relative estimation error and, more appropriately, the concept of a visibility length, a measure of how far upstream a sensor is able to accurately estimate the flow state. It has been demonstrated that a strongly convective system is characterized by a correspondingly small visibility length. In fact, in the latter case the optimal sensor placement has been found upstream of the actuators, and only this configuration was found to yield an efficient control performance. This upstream sensor placement suggests the use of a feed-forward approach for fluid systems with strong convection. Furthermore, treating upstream sensors as inputs in the identification procedure results in a very efficient and robust control. When validated on the Ginzburg–Landau model this technique is effective, and it is comparable to the optimal upper bound, given by full-state control, when the amplifier behaviour becomes convection-dominated. These concepts and findings have been extended and verified for flow over a backward-facing step at a Reynolds number 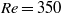$\mathit{Re}= 350$. Environmental noise has been introduced by three independent, localized sources. A very satisfactory control of the Kelvin–Helmholtz instability has been obtained with a one-order-of-magnitude reduction in the averaged perturbation norm. The above observations have been further confirmed by examining a low-order model problem that mimics a convection-dominated flow but allows the explicit computation of control-relevant measures such as observability. This study casts doubts on the usefulness of the asymptotic notion of observability for convection-dominated flows, since such flows are governed by transient effects. Finally, it is shown that the feed-forward approach is equivalent to an optimal linear–quadratic–Gaussian control for spy sensors placed sufficiently far upstream or for sufficiently convective flows. The control design procedure presented in this paper, consisting of data-based subspace identification and feed-forward control, was found to be effective and robust. Its implementation in a real physical experiment may confidently be carried out.

JFM classification

Flow Control: Control theory Flow Control: Flow Control Flow Control: Instability control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 522 - 565
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagheri, S., Brandt, L. & Henningson, D. S. 2009a Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.CrossRefGoogle Scholar
Bagheri, S., Henningson, D. S., Hoepffner, J. & Schmid, P. J. 2009b Input–output analysis and control design applied to a linear model of spatially developing flows. Appl. Mech. Rev. 62 (2), 020803.CrossRefGoogle Scholar
Barbagallo, A. 2011 Model reduction and closed-loop control of oscillator and noise-amplifier flows. PhD thesis, Ecole Polytechnique, Palaiseau, France.Google Scholar
Barbagallo, A., Dergham, G., Sipp, D., Schmid, P. J. & Robinet, J.-C. 2012 Closed-loop control of unsteadiness over a rounded backward-facing step. J. Fluid Mech. 703, 326–362.CrossRefGoogle Scholar
Barkley, D. M., Gomes, M. G. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
Bewley, T. R. 2001 Flow control: new challenges for a new renaissance. Prog. Aerosp. Sci. 37 (1), 21–58.CrossRefGoogle Scholar
Bewley, T. R. & Liu, S. 1998 Optimal and robust control and estimation of linear paths to transition. J. Fluid Mech. 365, 305–349.CrossRefGoogle Scholar
Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008 Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.CrossRefGoogle Scholar
Calvet, J. P. & Arkun, Y. 1988 Feedforward and feedback linearization of nonlinear system and its implementation using internal model control (IMC). Ind. Engng Chem. Res. 27 (10), 1822–1831.CrossRefGoogle Scholar
Cattafesta, L., Williams, D., Rowley, C. & Alvi, F. 2003 Review of active control of flow-induced cavity resonance. AIAA Paper 2003-3567.CrossRefGoogle Scholar
Chen, K. K. & Rowley, C. W. 2011 ${H}_{2} $ optimal actuator and sensor placement in the linearised complex Ginzburg–Landau system. J. Fluid Mech. 681, 241–260.CrossRefGoogle Scholar
Chevalier, M., Hœpffner, J., Akervik, E. & Henningson, D. S. 2007 Linear feedback control and estimation applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 588, 163–187.CrossRefGoogle Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37 (1), 357–392.CrossRefGoogle Scholar
Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1987 Models of hydrodynamic resonances in separated shear flows. In Proceeding of the 6th Symposium on Turbulent Shear Flows, September 7–9, Toulouse, France.Google Scholar
Favoreel, W., De Moor, B., Gevers, M. & Van Overschee, P. 1998 Model-free subspace-based LQG-design. Tech. Rep., Katholieke Universiteit Leuven.Google Scholar
Friedland, B. 1986 Control System Design, Introduction to State-Space Methods. Dover.Google Scholar
Greenblatt, D. & Wygnanski, I. J. 2000 The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 36 (7), 487–545.CrossRefGoogle Scholar
Henning, L. & King, R. 2007 Robust multivariable closed-loop control of a turbulent backwardfacing step flow. J. Aircraft 44, 201–208.CrossRefGoogle Scholar
Hervé, A., Sipp, D., Schmid, P. J. & Samuelides, M. 2010 Reduced order models for control design using system identification. In Proceedings of the 8th European Fluid Mechanics Conference, September.Google Scholar
Hervé, A., Sipp, D., Schmid, P. J. & Samuelides, M. 2012 A physics-based approach to flow control using system identification. J. Fluid Mech. 702, 26–58.CrossRefGoogle Scholar
Högberg, M., Bewley, T. R. & Henningson, D. S. 2003 Linear feedback control and estimation of transition in plane channel flow. J. Fluid Mech. 481, 149–175.CrossRefGoogle Scholar
Högberg, M. & Henningson, D. S. 2002 Linear optimal control applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 470, 151–179.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Joshi, S. S., Speyper, J. L. & Kim, J. 1997 A systems theory approach to the feedback stabilization of infinitesimal and finite-amplitude disturbances in plane Poiseuille flow. J. Fluid Mech. 332, 157–184.CrossRefGoogle Scholar
Joslin, R. D. 1998 Aircraft laminar flow control. Annu. Rev. Fluid Mech. 30 (1), 1–29.CrossRefGoogle Scholar
Juang, J.-N., Phan, M., Horta, L. G. & Longman, R. W. 1991 Identification of observer/Kalman filter Markov parameters – theory and experiments. J. Guid. Control Dyn. 16 (2), 320–329.CrossRefGoogle Scholar
Kalman, R. E. 1960 A new approach to linear filtering and prediction problems. Trans. ASME: J. Basic Engng 82, 35–45.CrossRefGoogle Scholar
Kegerise, M., Cabell, O. H. & Cattafesta, L. N. 2004 Real-time adaptive control of flow-induced cavity tones (invited). AIAA Paper 2004-0572.CrossRefGoogle Scholar
Kerstens, W., Pfeiffer, J., Williams, D., King, R. & Colonius, T. 2011 Closed-loop control of lift for longitudinal gust suppression at low Reynolds numbers. AIAA J. 49 (8).CrossRefGoogle Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39 (1), 383–417.CrossRefGoogle Scholar
Lanzerstorfer, D. & Kuhlmann, H. C. 2012 Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.CrossRefGoogle Scholar
Larimore, W. E. 1983 System identification, reduced order filtering and modelling via canonical variate analysis. In Proceedings of the Conference on Decision and Control, IEEE, 22–24 June, pp. 445–451.Google Scholar
Larimore, W. E. 1990 Canonical variate analysis in identification, filtering, and adaptive control. In Proceedings of the 29th IEEE Conference on Decision and Control, 5–7 December, Honolulu, Hawaii, vol. 2. pp. 596–604.CrossRefGoogle Scholar
de Larminat, P. 2002 Analyse des Systèmes Linéaires. Hermes Science.Google Scholar
Lauga, E. & Bewley, T. R. 2004 Performance of a linear robust control strategy on a nonlinear model of spatially developing flows. J. Fluid Mech. 512, 343–374.CrossRefGoogle Scholar
Ljung, L. 1999 System Identification: Theory for the User, 2nd edn. Prentice-Hall PTR.Google Scholar
Ma, Z., Ahuja, S. & Rowley, C. 2011 Reduced-order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 25, 233–247.CrossRefGoogle Scholar
McKelvey, T. 1994 On state-space models in system identification. PhD thesis, Department of Electrical Engineering, Linköping University, Sweden.Google Scholar
Meckl, P. H. & Seering, W. P. 1986 Feedforward control techniques to achieve fast settling time in robots. In American Control Conference, IEEE, 18–20 June, 1986, pp. 1913–1918.CrossRefGoogle Scholar
Noack, B., Morzynski, M. & Tadmor, G. 2011 Reduced-Order Modelling for Flow Control. Springer.CrossRefGoogle Scholar
Qin, S. J. 2006 An overview of subspace identification. Comput. Chem. Engng 30, 1502–1513.CrossRefGoogle Scholar
Qin, S. & Badgwell, T. 2003 A survey of industrial model predictive control technology. Control Engng Pract. 11 (7), 733–764.CrossRefGoogle Scholar
Rathnasingham, R. & Breuer, K. S. 2003 Active control of turbulent boundary layers. J. Fluid Mech. 495, 209–233.CrossRefGoogle Scholar
Semeraro, O., Bagheri, S., Brandt, L. & Henningson, D. S. 2011 Feedback control of three-dimensional optimal disturbances using reduced-order models. J. Fluid Mech. 677, 63–102.CrossRefGoogle Scholar
Sharma, A. S., Morrison, J. F., McKeon, B. J., Limebeer, D. J. N., Koberg, W. H. & Sherwin, S. J. 2011 Relaminarisation of $R{e}_{\tau } = 100$ channel flow with globally stabilising linear feedback control. Phys. Fluids 23 (12), 125105.CrossRefGoogle Scholar
Skogestad, S. & Postlethwaite, I. 1996 Multivariable Feedback Control, Analysis and Design. John Wiley & Sons.Google Scholar
Thomas, B., Soleimani-Mohseni, M. & Fahln, P. 2005 Feed-forward in temperature control of buildings. Energy Build. 37 (7), 755–761.CrossRefGoogle Scholar
Tian, Y., Song, Q. & Cattafesta, L. 2006 Adaptive feedback control of flow separation. AIAA Paper 2006-3016.CrossRefGoogle Scholar
Van Overschee, P. & De Moor, B. 1994 N4SID: subspace algorithms for the identification of combined deterministic–stochastic systems. Automatica 30 (1), 75–93.CrossRefGoogle Scholar
Van Overschee, P. & De Moor, B. 1995 A unifying theorem for three subspace system identification algorithms. Automatica 31 (12), 1853–1864.CrossRefGoogle Scholar
Van Overschee, P. & De Moor, B. 1996 Subspace Identification for Linear Systems. Kluwer.CrossRefGoogle Scholar
Verhaegen, M. & Deprettere, E. 1991 A fast, recursive MIMO state space model identification algorithm. In Proceedings of the 30th IEEE Conference on Decision and Control, 11–13 December 1991, vol. 2, pp. 1349–1354. IEEE.Google Scholar
Zeng, J. & de Callafon, R. 2003 Feedforward noise cancellation in an airduct using generalized fir filter estimation. In Proceedings of the 42nd IEEE Conference on Decision and Control, 9–12 December 2003, vol. 6, pp. 6392–6397. IEEE.Google Scholar
Zhou, K., Doyle, J. C. & Glover, K. 1996 Robust and Optimal Control. Prentice-Hall.Google Scholar