Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T08:53:05.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent structures in the linearized impulse response of turbulent channel flow

Published online by Cambridge University Press:  30 January 2019

Sabarish B. Vadarevu Open the ORCID record for Sabarish B. Vadarevu [Opens in a new window] ,
Sean Symon Open the ORCID record for Sean Symon [Opens in a new window] ,
Simon J. Illingworth Open the ORCID record for Simon J. Illingworth [Opens in a new window]  and
Ivan Marusic Open the ORCID record for Ivan Marusic [Opens in a new window]
Sabarish B. Vadarevu
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
Sean Symon
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
Simon J. Illingworth*
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
Ivan Marusic
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

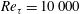We study the evolution of velocity fluctuations due to an isolated spatio-temporal impulse using the linearized Navier–Stokes equations. The impulse is introduced as an external body force in incompressible channel flow at $Re_{\unicode[STIX]{x1D70F}}=10\,000$. Velocity fluctuations are defined about the turbulent mean velocity profile. A turbulent eddy viscosity is added to the equations to fix the mean velocity as an exact solution, which also serves to model the dissipative effects of the background turbulence on large-scale fluctuations. An impulsive body force produces flow fields that evolve into coherent structures containing long streamwise velocity streaks that are flanked by quasi-streamwise vortices; some of these impulses produce hairpin vortices. As these vortex–streak structures evolve, they grow in size to be nominally self-similar geometrically with an aspect ratio (streamwise to wall-normal) of approximately 10, while their kinetic energy density decays monotonically. The topology of the vortex–streak structures is not sensitive to the location of the impulse, but is dependent on the direction of the impulsive body force. All of these vortex–streak structures are attached to the wall, and their Reynolds stresses collapse when scaled by distance from the wall, consistent with Townsend’s attached-eddy hypothesis.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 1190 - 1203
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.10.1063/1.2717527Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.10.1017/jfm.2017.357Google Scholar
Cess, R. D.1958 A survey of the literature on heat transfer in turbulent tube flow. Tech. Rep. 8–0529–R24. Westinghouse Research.Google Scholar
Codrignani, A. R.2014 Impulse response in a turbulent channel flow. PhD thesis, Politec. Milano.Google Scholar
Del Álamo, J. C. & Jimenez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.10.1017/S0022112006000607Google Scholar
Eitel-Amor, G., Örlü, R., Schlatter, P. & Flores, O. 2015 Hairpin vortices in turbulent boundary layers. Phys. Fluids 27 (2), 025108.10.1063/1.4907783Google Scholar
Farano, M., Cherubini, S., Robinet, J.-C. & De Palma, P. 2017 Optimal bursts in turbulent channel flow. J. Fluid Mech. 817, 35–60.10.1017/jfm.2017.107Google Scholar
Halcrow, J., Gibson, J. F., Cvitanović, P. & Viswanath, D. 2009 Heteroclinic connections in plane Couette flow. J. Fluid Mech. 621, 365–376.10.1017/S0022112008005065Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.10.1017/S0022112010002892Google Scholar
Henningson, D. S. & Reddy, S. C. 1994 On the role of linear mechanisms in transition to turbulence. Phys. Fluids 6 (3), 1396–1398.10.1063/1.868251Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.10.1063/1.2162185Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.10.1017/S0022112085003147Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.10.1017/jfm.2015.24Google Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1 (6), 064401.10.1103/PhysRevFluids.1.064401Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.10.1017/S0022112009992151Google Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.10.1017/S0022112010003629Google Scholar
Illingworth, S. J., Monty, J. P. & Marusic, I. 2018 Estimating large-scale structures in wall turbulence using linear models. J. Fluid Mech. 842, 146–162.10.1017/jfm.2018.129Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.10.1017/S0022112091002033Google Scholar
Jovanović, M. & Bamieh, B. 2001 The spatio-temporal impulse response of the linearized Navier–Stokes equations. In Proc. 40th IEEE Conf. Decision and Control, pp. 1948–1953.Google Scholar
Jovanović, M. R.2004 Modeling, analysis, and control of spatially distributed systems. PhD thesis, University of California at Santa Barbara.Google Scholar
Kim, J. & Lim, J. 2000 A linear process in wall-bounded turbulent shear flows. Phys. Fluids 12 (8), 1885–1888.10.1063/1.870437Google Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.10.1017/S0022112090002105Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.10.1017/jfm.2011.524Google Scholar
Luchini, P., Quadrio, M. & Zuccher, S. 2006 The phase-locked mean impulse response of a turbulent channel flow. Phys. Fluids 18 (12), 121702.10.1063/1.2409729Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946Google Scholar
McKeon, B. J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.10.1017/jfm.2017.115Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.10.1017/S002211201000176XGoogle Scholar
Moarref, R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2013 Model-based scaling of the streamwise energy density in high Reynolds number turbulent channels. J. Fluid Mech. 734, 275–316.10.1017/jfm.2013.457Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.10.1017/S0022112095003351Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 015109.10.1063/1.3068760Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.10.1017/S0022112072000679Google Scholar
Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’s theory. J. Fluid Mech. 27 (2), 253–272.10.1017/S0022112067000308Google Scholar
Towne, A., Yang, X. & Lozano-Durán, A. 2018 Approximating space–time flow statistics from a limited set of known correlations. AIAA Aviation Forum paper 4043.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Waleffe, F. 1995 Transition in shear flows. Nonlinear normality versus non-normal linearity. Phys. Fluids 7 (12), 3060–3066.10.1063/1.868682Google Scholar
Zare, A., Jovanović, M. R. & Georgiou, T. T. 2017 Colour of turbulence. J. Fluid Mech. 812, 636–680.10.1017/jfm.2016.682Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.10.1017/S002211209900467XGoogle Scholar