Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T01:01:37.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Bistability and hysteresis induced by form drag in nonlinear subcritical and supercritical double-diffusive Lapwood convection in shallow porous enclosures

Published online by Cambridge University Press:  06 January 2017

Redha Rebhi ,
Mahmoud Mamou  and
Patrick Vasseur
Redha Rebhi
Affiliation:
Laboratoire de Mécanique Physique et Modélisation Mathématique (LMP2M), Université Dr. Yahia Farès de Médéa, Quartier Ain D’Heb, Médéa 26000, Algérie
Mahmoud Mamou*
Affiliation:
Aerodynamics Laboratory, NRC Aerospace, National Research Council Canada, Ottawa, Ontario K1A OR6, Canada
Patrick Vasseur
Affiliation:
Ecole Polytechnique, Université de Montréal, C.P. 6079, Succ. Centre-ville, Montréal, Québec, H3C 3A7, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers natural Lapwood convection in a shallow porous cavity filled with a binary fluid. The investigation is mainly focused on the nonlinear behaviour of subcritical convection and the bistability phenomenon caused by the combined effects of porous medium form drag and double-diffusive convection. The Dupuit–Darcy model, which includes the effect of the form drag at high Reynolds flow, is used to describe the convective flow in the porous matrix. The enclosure is subject to vertical temperature and concentration gradients. The governing parameters of the problem under study are the Rayleigh number, 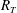$R_{T}$, the buoyancy ratio, 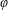$\unicode[STIX]{x1D711}$, the Lewis number, 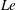$Le$, the form drag coefficient, (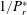$1/P_{r}^{\ast }$), where 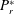$P_{r}^{\ast }$ is a modified Prandtl number, and the aspect ratio of the cavity, 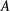$A$. An analytical solution, valid for shallow enclosures (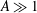$A\gg 1$), is derived on the basis of the parallel flow approximation. Among other things, this work focuses on the effects of the form drag parameter on the convective flows that occur when the thermal and solutal buoyancy forces are opposing each other. For this situation, in the absence of the form drag effect, the onset of motion is known to occur at a subcritical Rayleigh number, 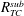$R_{TC}^{sub}$, which depends upon 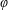$\unicode[STIX]{x1D711}$ and 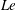$Le$ only. The effects of 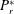$P_{r}^{\ast }$ on 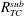$R_{TC}^{sub}$ and on the subsequent convective heat and mass transfer rates are found to be significant. A new bistability phenomenon arises when the onset of subcritical convection is shifted close to or beyond the threshold of supercritical convection, whether heating or cooling isothermally or upon applying constant heat and solute fluxes, regardless of the enclosure aspect ratio value. It is demonstrated, on the basis of linear stability theory, that the form drag parameter has a stabilizing effect and considerably affects the threshold for Hopf bifurcation, 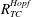$R_{TC}^{Hopf}$, which characterizes the transition from steady to unsteady convection. In the range of governing parameters considered in this study, the heat, solute and flow characteristics predicted by the analytical model are found to agree well with the numerical study of the full governing equations.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in porous media Convection: Double diffusive convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 463 - 500
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alloui, Z., Bennacer, R. & Vasseur, P. 2009 Variable permeability effect on convection in binary mixtures saturating a porous layer. Intl J. Heat Mass Transfer 45, 1117–1127.Google Scholar
Alloui, Z. & Vasseur, P. 2013 Onset of Marangoni convection and multiple solutions in a power-law fluid layer under a zero gravity environment. Intl J. Heat Mass Transfer 58, 43–52.CrossRefGoogle Scholar
Bahloul, A., Boutana, N. & Vasseur, P. 2003 Double-diffusive and Soret-induced convection in a shallow horizontal porous layer. J. Fluid Mech. 491, 325–352.Google Scholar
Bahloul, A., Vasseur, P. & Robillard, L. 2007 Convection of a binary fluid saturating a shallow porous cavity subjected to cross heat fluxes. J. Fluid Mech. 574, 317–342.Google Scholar
Beavers, G. S., Sparrow, E. M. & Rodenz, D. E. 1973 Influence of bed size on the flow characteristics and porosity of randomly packed beds of spheres. Trans. ASME J. Appl. Mech. 40, 655–660.Google Scholar
Bhadauria, B. S. 2007 Double diffusive convection in a porous medium with modulated temperature on the boundaries. Trans. Porous Med. 70, 191–211.Google Scholar
Brinkman, H. C. 1949 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1, 27–34.Google Scholar
Dupuit, A. J. E. J. 1863 Études Théoriques et Pratiques sur le Mouvement des Eaux dans les Canaux Découverts et à Travers les Terrains Perméables. Victor Dalmont.Google Scholar
Forchheimer, P. 1901 Wasserbewegung durch boden. Z. Verein. Deutsch. Ing. 45, 1782–1788.Google Scholar
Gaikwad, S. N. & Kamble, S. S. 2012 Soret effect on linear DDC in a horizontal sparsely packed porous layer. Intl J. Phys. Math. Sci. 2 (2), 97–104.Google Scholar
Ingham, D. B. & Pop, I.(Eds) 1998 Transport Phenomena in Porous Media I. Pergamon.Google Scholar
Ingham, D. B. & Pop, I.(Eds) 2005 Transport Phenomena in Porous Media III. Elsevier.Google Scholar
Joseph, D. D., Nield, D. A. & Papanicolaou, G. 1982 Nonlinear equation governing flow in a saturated porous medium. Water Resour. Res. 18, 1049–1052; and 19, 591.Google Scholar
Kalla, L., Mamou, M., Vasseur, P. & Robillard, L. 2001 Multiple solutions for double diffusive convection in a shallow porous cavity with vertical fluxes of heat and mass. Intl J. Heat Mass Transfer 44, 4493–4504.Google Scholar
Karimi-Fard, M., Charrier-Mojtabi, M. C. & Vafai, K. 1997 Non-Darcian effects on double-diffusive convection within a porous medium. Numer. Heat Transfer A 31, 837–852.Google Scholar
Khanafer, K. & Vafai, K. 2002 Double-diffusive mixed convection in a lid-driven enclosure filled with a fluid-saturated porous medium. Numer. Heat Transfer A 42, 465–486.CrossRefGoogle Scholar
Kimura, S., Vynnycky, M. & Alavyoon, F. 1995 Unicellular natural circulation in a shallow horizontal porous layer heated from below by a constant flux. J. Fluid Mech. 294, 231–257.Google Scholar
Lage, J. L. 1998 The fundamental theory of flow through permeable media from Darcy to turbulence. In Transport Phenomena in Porous Media (ed. Ingham, D. B. & Pop, I.), pp. 1–30. Pergamon.Google Scholar
Lasseux, D., Abbasian Arani, A. A. & Ahmadi-Senichault, A. 2011 On the stationary macroscopic inertial effects for one phase flow in ordered and disordered porous media. Phys. Fluids 23 (7), 073103.Google Scholar
Mahidjiba, A., Bennacer, R. & Vasseur, P. 2006 Flows in a fluid layer induced by the combined action of a shear stress and the Soret effect. Intl J. Heat Mass Transfer 49, 1403–1411.Google Scholar
Mahidjiba, A., Mamou, M. & Vasseur, P. 2000 Onset of double-diffusive convection in a rectangular porous cavity subject to mixed boundary conditions. Intl J. Heat Mass Transfer 43, 1505–1522.CrossRefGoogle Scholar
Mamou, M. 2003 Stability analysis of the perturbed rest state and of the finite amplitude steady double-diffusive convection in a shallow porous enclosure. Intl J. Heat Mass Transfer 46, 2263–2277.Google Scholar
Mamou, M. & Vasseur, P. 1999 Thermosolutal bifurcation phenomena in porous enclosures subject to vertical temperature and concentration gradients. J. Fluid Mech. 395, 61–87.Google Scholar
Mansour, A., Amahmid, A. & Hasnaoui, M. 2008 Soret effect on thermosolutal convection developed in a horizontal shallow porous layer salted from below and subject to cross fluxes of heat. Intl J. Heat Fluid Flow 29, 306–314.Google Scholar
Mansour, A., Amahmid, A., Hasnaoui, M. & Mamou, M. 2007 Onset of thermosolutal convection in a shallow porous layer heated and salted from below and subject to a horizontal heat flux balanced by a Soret mass flux. Intl J. Heat Mass Transfer 50, 2148–2160.Google Scholar
Motsa, S. S. 2008 On the onset of convection in a porous layer in the presence of Dufour and Soret effects. SAMSA J. Pure Appl. Maths 3, 58–65.Google Scholar
Nield, D. A. 1968 Onset of thermohaline convection in a porous medium. Water Resour. Res. 4, 553–560.Google Scholar
Nield, D. A. 2000 Resolution of a paradox involving viscous dissipation and nonlinear drag in a porous medium. Trans. Porous Med. 41, 349–357.Google Scholar
Nield, D. A. & Bejan, A.(Eds) 2013 Convection in Porous Media, 4th edn. Springer.Google Scholar
Nield, D. A., Manole, D. M. & Lage, J. L. 1993 Convection induced by inclined thermal and solutal gradients in a shallow horizontal layer of porous medium. J. Fluid Mech. 257, 559–574.CrossRefGoogle Scholar
Rebhi, R., Mamou, M. & Alliche, M. 2014 Form drag effect and Hopf bifurcation in Dupuit–Darcy thermal convection in a shallow well-packed porous enclosure. Phys. Fluids 26, 074104.Google Scholar
Rebhi, R., Mamou, M., Vasseur, P. & Alliche, M. 2016 Form drag effect on the onset of non-linear convection and Hopf bifurcation in binary fluid saturating a tall porous cavity. Intl J. Heat Mass Transfer 100, 178–190.Google Scholar
Shivakumara, I. S. & Sumithra, R. 1999 Non-Darcian effects on double diffusive convection in a sparsely packed porous medium. Acta Mech. 132, 113–127.Google Scholar
Taunton, J. W., Lightfoot, E. N. & Green, T. 1972 Thermohaline instability and salt fingers in a porous medium. Phys. Fluids 15, 748–753.Google Scholar
Vadasz, P.(Ed.) 2008 Emerging Topics in Heat and Mass Transfer in Porous Media. Springer.Google Scholar
Vafai, K.(Ed.) 2005 Handbook of Porous Media. Taylor & Francis.Google Scholar

Rebhi et al. supplementary movie

ψp

Download Rebhi et al. supplementary movie(Video)
Video 2.8 MB

Rebhi et al. supplementary movie

Tp

Download Rebhi et al. supplementary movie(Video)
Video 2.2 MB

Rebhi et al. supplementary movie

Sp

Download Rebhi et al. supplementary movie(Video)
Video 2.8 MB