Published online by Cambridge University Press: 18 September 2013
Numerical simulations and laboratory experiments were jointly conducted to investigate a bathtub vortex under the influence of a protruding cylinder in a rotating tank. In the set-up, a central drain hole is placed at the bottom of the tank and a top-down cylinder is suspended from the rigid top lid, with fluid supplied from the sidewall for mass conservation. The cylinder is protruded to produce the Taylor column effect. The flow pattern depends on the Rossby number ( $\mathit{Ro}= U/ fR$), the Ekman number (
$\mathit{Ro}= U/ fR$), the Ekman number (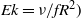 $\mathit{Ek}= \nu / f{R}^{2} )$ and the height ratio,
$\mathit{Ek}= \nu / f{R}^{2} )$ and the height ratio, 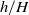 $h/ H$, where
$h/ H$, where 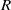 $R$ is the radius of the cylinder,
$R$ is the radius of the cylinder, 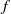 $f$ is the Coriolis parameter,
$f$ is the Coriolis parameter,  $\nu $ is the kinematic viscosity of the fluid,
$\nu $ is the kinematic viscosity of the fluid, 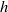 $h$ is the vertical length of the cylinder and
$h$ is the vertical length of the cylinder and 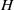 $H$ is the height of the tank. It is found appropriate to choose
$H$ is the height of the tank. It is found appropriate to choose 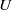 $U$ to be the average inflow velocity of fluid entering the column beneath the cylinder. Steady-state solutions obtained by numerically solving the Navier–Stokes equations in the rotating frame are shown to have a good agreement with flow visualizations and particle tracking velocimetry (PTV) measurements. It is known that at
$U$ to be the average inflow velocity of fluid entering the column beneath the cylinder. Steady-state solutions obtained by numerically solving the Navier–Stokes equations in the rotating frame are shown to have a good agreement with flow visualizations and particle tracking velocimetry (PTV) measurements. It is known that at 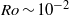 $\mathit{Ro}\sim 1{0}^{- 2} $, the central downward flow surrounded by the neighbouring Ekman pumping forms a classic one-celled bathtub vortex structure when there is no protruding cylinder (
$\mathit{Ro}\sim 1{0}^{- 2} $, the central downward flow surrounded by the neighbouring Ekman pumping forms a classic one-celled bathtub vortex structure when there is no protruding cylinder (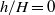 $h/ H= 0$). The influence of a suspended cylinder (
$h/ H= 0$). The influence of a suspended cylinder (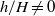 $h/ H\not = 0$) leads to several findings. The bathtub vortex exhibits an interesting two-celled structure with an inner Ekman pumping (EP) and an outer up-drafting motion, termed Taylor upwelling (TU). The two regions of up-drafting motion are separated by a notable finite-thickness structure, identified as a (thin-walled) Taylor column. The thickness
$h/ H\not = 0$) leads to several findings. The bathtub vortex exhibits an interesting two-celled structure with an inner Ekman pumping (EP) and an outer up-drafting motion, termed Taylor upwelling (TU). The two regions of up-drafting motion are separated by a notable finite-thickness structure, identified as a (thin-walled) Taylor column. The thickness 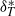 ${ \delta }_{T}^{\ast } $ of the Taylor column is found to be well correlated to the height ratio and the Ekman number by
${ \delta }_{T}^{\ast } $ of the Taylor column is found to be well correlated to the height ratio and the Ekman number by 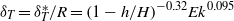 ${\delta }_{T} = { \delta }_{T}^{\ast } / R= {(1- h/ H)}^{- 0. 32} {\mathit{Ek}}^{0. 095} $. The Taylor column presents a barrier to the fluid flow such that the fluid from the inlet may only flow into the inner region through the narrow gaps, one above the Taylor column and one beneath it (conveniently called Ekman gaps). As a result, five types of routes along which the fluid may flow to and exit at the drain hole could be identified for the multi-celled vortex structure. Moreover, the flow rates associated with the five routes were calculated and compared to help understand the relative importance of the component flow structures. The weaker influence of the Taylor column effect on the bathtub vortex at
${\delta }_{T} = { \delta }_{T}^{\ast } / R= {(1- h/ H)}^{- 0. 32} {\mathit{Ek}}^{0. 095} $. The Taylor column presents a barrier to the fluid flow such that the fluid from the inlet may only flow into the inner region through the narrow gaps, one above the Taylor column and one beneath it (conveniently called Ekman gaps). As a result, five types of routes along which the fluid may flow to and exit at the drain hole could be identified for the multi-celled vortex structure. Moreover, the flow rates associated with the five routes were calculated and compared to help understand the relative importance of the component flow structures. The weaker influence of the Taylor column effect on the bathtub vortex at 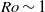 $\mathit{Ro}\sim 1$ or even higher
$\mathit{Ro}\sim 1$ or even higher 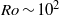 $\mathit{Ro}\sim 1{0}^{2} $ is also discussed.
$\mathit{Ro}\sim 1{0}^{2} $ is also discussed.