Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T09:08:06.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Anisotropic pressure correlation spectra in turbulent shear flow

Published online by Cambridge University Press:  02 February 2012

Yoshiyuki Tsuji  and
Yukio Kaneda
Yoshiyuki Tsuji*
Affiliation:
Department of Energy Engineering and Science, Graduate School of Engineering, Nagoya University, Chikusa-ku, Nagoya 464-8603, Japan
Yukio Kaneda
Affiliation:
Department of Computational Science and Engineering, Graduate School of Engineering, Nagoya University, Chikusa-ku, Nagoya 464-8603, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

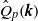We measured the correlation spectrum of pressure fluctuations in a driving mixing layer with a Taylor-scale Reynolds number 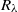up to by a newly developed pressure probe with spatial and temporal resolutions that are sufficient to analyse inertial-subrange statistics. The influence of the mean velocity gradient tensor 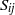in the mixing layer, which is almost constant near its centreline, is studied using an idea similar to that underlying the linear response theory developed in statistical mechanics for systems at or near thermal equilibrium. 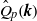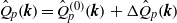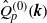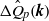If we write the spectrum as , where is the isotropic Kolmogorov spectrum in the absence of mean shear, then for small the deviation due to the shear is approximately linear and is determined by a few non-dimensional universal constants in addition to 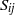, 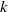and the mean energy dissipation rate. We also measured the pressure–velocity and velocity–velocity correlation spectra. Deviations from isotropy due to shear are shown to be approximately proportional to 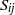at large .

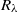JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 50 - 77
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arad, I., Dhruva, B., Kurien, S., L’vov, V. S., Procaccia, I. & Sreenivasan, K. R. 1998 Extraction of anisotropic contribution in turbulent flows. Phys. Rev. Lett. 81, 5330–5333.CrossRefGoogle Scholar
2. Arad, I., L’vov, V. S. & Procaccia, I. 1999 Correlation functions in isotropic and anisotropic turbulence: the role of the symmetry group. Phys. Rev. E 59, 6753–6765.CrossRefGoogle ScholarPubMed
3. Batchelor, G. K. 1951 Pressure fluctuations in isotropic turbulence. Proc. Camb. Phil. Soc. 47, 359–374.CrossRefGoogle Scholar
4. Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28, 2034–2042.Google Scholar
5. Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.CrossRefGoogle Scholar
6. Borue, V. & Orszag, S. A. 1996 Numerical study of three-dimensional Kolmogorov flow at high Reynolds numbers. J. Fluid Mech. 306, 293–323.Google Scholar
7. Browne, L. W. B., Antonia, R. A. & Chua, L. P. 1989 Calibration of x-probes for turbulent flow measurements. Exp. Fluids 7, 201–208.Google Scholar
8. Cao, N., Chen, S. & Doolen, G. D. 1999 Statistics and structures of pressure in isotropic turbulence. Phys. Fluids 11, 2235–2250.CrossRefGoogle Scholar
9. Casciola, C. M., Gualtieri, P., Jacob, B. & Piva, R. 2005 Scaling properties in the production range of shear dominated flows. Phys. Rev. Lett. 95, 024503.Google Scholar
10. Casciola, C. M., Gualtieri, P., Jacob, B. & Piva, R. 2007 The residual anisotropy at small scales in high shear turbulence. Phys. Fluids 19, Art. 101704.Google Scholar
11. Champagne, F. H., Pao, Y. H. & Wygnanski, I. J. 1976 On the two-dimensional mixing region. J. Fluid Mech. 74, 209–250.Google Scholar
12. Corrsin, S. 1958 Local isotropy in turbulent shear flow. NACA R & M 58B11.Google Scholar
13. Frish, U. 1995 Turbulence. Cambridge University Press.Google Scholar
14. George, W. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.CrossRefGoogle Scholar
15. George, W. K., Beuther, P. D. & Arndt, R. E. A. 1984 Pressure spectra in turbulent free shear flows. J. Fluid Mech. 148, 155–191.Google Scholar
16. Gotoh, T. & Fukayama, D. 2001 Pressure spectrum in homogeneous turbulence. Phys. Rev. Lett. 86, 3775–3778.Google Scholar
17. Gotoh, T. & Rogallo, R. S. 1999 Intermittency and scaling of pressure at small-scales in forced isotropic turbulence. J. Fluid Mech. 396, 257–285.CrossRefGoogle Scholar
18. Heisenberg, W. 1948 Zür statistischen theorie der turbulenz. Z. Phys. 124, 628–657.Google Scholar
19. Hill, R. J. 2002 Scaling of acceleration in locally isotropic turbulence. J. Fluid Mech. 452, 361–370.Google Scholar
20. Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
21. Inoue, E. 1951 The application of the turbulence theory to the large-scale atmospheric phenomena. Geophys. Mag. 23, 1–14.Google Scholar
22. Ishida, T. & Kaneda, Y. 2007 Small-scale anisotropy in magnetohydrodynamic turbulence under a strong uniform magnetic field. Phys. Fluids 19, 075104, 10 pages.CrossRefGoogle Scholar
23. Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2003 Spectra of energy dissipation, enstropy and pressure by high-resolution direct numerical simulations of turbulence in a periodic box. J. Phys. Soc. Japan 72, 983–986.CrossRefGoogle Scholar
24. Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
25. Ishihara, T., Yoshida, K. & Kaneda, Y. 2002 Anisotropic velocity correlation spectrum at small-scales in a homogeneous turbulent shear flow. Phys. Rev. Lett. 88, 154501–1–4.CrossRefGoogle Scholar
26. Jacob, B., Casciola, C. M., Talamelli, A. & Alfredsson, P. H. 2008 Scaling of mixed structure functions in turbulent boundary layers. Phys. Fluids 20, art. 045101.CrossRefGoogle Scholar
27. Jones, B. G., Adrian, R. J., Nithiandan, C. K. & Planchon, H. P. 1979 Spectra of turbulent static pressure fluctuation in jet mixing layers. AIAA J. 17, 449–457.Google Scholar
28. Kaneda, Y. & Ishihara, T. 2009 Universality in statistics at small scales of turbulence -a study by high resolution DNS. In Notes Numerical Fluid Mechanics and Multidisciplinary Design (ed. Deville, M., Le, T.-H. & Sagaut, P. ). 105. pp. 55–76. Springer.Google Scholar
29. Kaneda, Y. & Morishita, K. 2011 Small-scale statistics and structure of Turbulence – in the light of high resolution direct numerical simulation –. In The Nature of Turbulence (ed. Davidson, P., Kaneda, Y. & Sreenivasan, K.R. ). Cambridge Unversity Press, (submitted).Google Scholar
30. Kaneda, Y. & Yoshida, K. 2004 Small-scale anisotropy in stably stratified turbulence. New J. Phys. 6, 34.CrossRefGoogle Scholar
31. Kim, J. & Antonia, R. A. 1993 Isotropy of the small-scales of turbulence at low Reynolds number. J. Fluid Mech. 251, 219–238.Google Scholar
32. Klebanoff, P. S. 1954 Characteristics of turbulence in a boundary later with zero pressure gradient. NACA Technical Note 3178.Google Scholar
33. Kobashi, Y. 1957 Measurements of pressure fluctuation in the wake of cylinder. J. Phys. Soc. Japan 12, 533–543.Google Scholar
34. Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
35. Kraichnan, R. H. 1956a Pressure field within homogeneous anisotropic turbulence. J. Acoust. Soc. Am. 28, 64–72.Google Scholar
36. Kraichnan, R. H. 1956b Pressure fluctuation in turbulent flow over a flat plate. J. Acoust. Soc. Am. 28, 378–390.Google Scholar
37. Kubo, R. 1966 The fluctuation-dissipation theorem. Rep. Prog. Phys. 29, 255–284.CrossRefGoogle Scholar
38. Kurien, S., L’vov, V. S., Procaccia, I. & Sreenivasan, K. R. 2000 Scaling structure of the velocity statistics in atmospheric boundary layers. Phys. Rev. E 61, 407–421.Google Scholar
39. La Porta, A., Voth, G. A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2001 Fluid particle accelerations in fully developed turbulence. Nature 409, 1017–1019.CrossRefGoogle ScholarPubMed
40. Lumley, J. L. 1965 Interpretation of time spectra measured in high-intensisty shear flows. Phys. Fluids 8, 1056–1062.Google Scholar
41. Lumley, J. L. 1967 Similarity and the turbulence energy spectrum. Phys. Fluids 10, 855–858.Google Scholar
42. Monin, M. S. & Yaglom, A. M. 1971 Statistical Fluid Mechanics, Vol. 2. The MIT Press.Google Scholar
43. Nakano, H. 1993 Linear response theory: a historical perspective. Intl J. Mod. Phys. 7, 2397–2467.CrossRefGoogle Scholar
44. Nelkin, M. 1994 Universality and scaling in fully developed turbulence. Adv. Phys. 43, 143–181.Google Scholar
45. Obukhoff, A. M. & Yaglom, A. M. 1951 The microstructure of turbulent flow. NACA Tech. Mem. 1350.Google Scholar
46. Ott, S. & Mann, J. 2000 An experimental investigation of the relative diffusion of particle pairs in three-dimensional turbulent flow. J. Fluid Mech. 422, 207–223.CrossRefGoogle Scholar
47. Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
48. Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6, 903–923.CrossRefGoogle Scholar
49. Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
50. Shen, X. & Warhaft, Z. 2000 The anisotropy of the small-scale structure in high Reynolds number turbulent shear flow. Phys. Fluids 12, 2976–2989.CrossRefGoogle Scholar
51. Smyth, W. D. & Moum, J. N. 2000 Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1343–1362.Google Scholar
52. Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
53. Sreenivasan, K. R. & Dhruva, B. 1998 Is there scaling in high-Reynolds-number turbulence? Progr. Theor. Phys. Suppl. 130, 103–120.Google Scholar
54. Sreenivasan, K. R. & Stolovitzky, G. 1996 Statistical dependence of inertila range properties on large scales in a high-Reynolds-number shear flow. Phys. Rev. Lett. 77, 2218–2221.CrossRefGoogle Scholar
55. Staicu, A., Vorselaars, B. & van de Water, W. 2003 Turbulence anisotropy and the SO(3) description. Phys. Rev. E 68, 046303–1–12.Google Scholar
56. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
57. Toyoda, K., Okamoto, T. & Shirahama, Y. 1993 Eduction of vortical structures by pressure measurements in noncircular jet. Fluid Mech. Appl. 21, 125–136.Google Scholar
58. Tsuji, Y. 2002 Anisotropy versus universality in shear flow turbulence. In Statistical Theories and Computational Approaches to Turbulence (ed. Kaneda, Y. & Gotoh, T. ). pp. 138–158. Springer.Google Scholar
59. Tsuji, Y. 2003 Large-scale anisotropy effect on small-scale statistics over rough wall turbulent boundary layers. Phys. Fluids 12, 3816–3828.Google Scholar
60. Tsuji, Y. 2007 Lagrangian acceleration measurement in fully developed turbulence. In Turbulent Shear Flow Phenomena 5, TU Munchen, Garching, Germany, 27–29 August, 2007, pp. 537–541.Google Scholar
61. Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.Google Scholar
62. Tsuji, Y. & Ishihara, T. 2003 Similarity scaling of pressure fluctuation in turbulence. Phys. Rev. E 68, 026309.Google Scholar
63. Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulation of isotropic turbulence. Phys. Fluids 11, 1208–1220.Google Scholar
64. Warhaft, Z. 2000 Passive scalars in turbulent flow. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
65. Wygnanski, I. & Fiedler, H. E. 1970 Two-dimensional mixing region. J. Fluid Mech. 41, 327–361.Google Scholar
66. Wyngaard, J. C. & Cote, O. R. 1972 Cospectral similarity in the atomospheric surface layer. J. R. Met Soc. 98, 590–603.Google Scholar
67. Yoshida, K., Ishihara, T. & Kaneda, Y. 2003 Anisotropic spectrum of homogeneous turbulent shear flow in a Lagrangian renormalized approximation. Phys. Fluids 15, 2385–2397.Google Scholar