Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T16:05:14.009Z Has data issue: false hasContentIssue false
  • English
  • Français

An experimental study of turbulent vortex rings in superfluid 4He

Published online by Cambridge University Press:  24 February 2020

P. Švančara Open the ORCID record for P. Švančara [Opens in a new window] ,
M. Pavelka Open the ORCID record for M. Pavelka [Opens in a new window]  and
M. La Mantia Open the ORCID record for M. La Mantia [Opens in a new window]
P. Švančara
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121  16 Prague, Czech Republic
M. Pavelka
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121  16 Prague, Czech Republic
M. La Mantia*
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121  16 Prague, Czech Republic
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

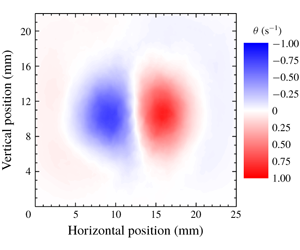
Macroscopic vortex rings are generated thermally in superfluid 4He, between 1.28 and 1.95 K, by applying a brief voltage pulse to a resistive heater located below a circular vertical tube 5 mm in diameter and 20 mm high. The rings form above the tube and propagate upward with velocities of the order of $10~\text{mm}~\text{s}^{-1}$, resulting in Reynolds numbers up to $10^{5}$. We visualize their cross-section, of size comparable with the tube diameter, by capturing the motions of relatively small solid deuterium particles, previously dispersed in the quiescent bath of superfluid 4He. We employ particle positions and velocities to compute the Lagrangian pseudovorticity, which can be seen as a measure of the ring strength and which allows us to identify and track these objects. We thus obtain time-dependent sizes, positions and velocities of the vortex rings. We show that, in the range of investigated parameters, these rings behave as if they were turbulent vortex rings moving in classical viscous fluids, at least in the direction of ring propagation. The outcome reinforces the view that the study of turbulent flows of superfluid 4He is not only interesting in its own right, but that it can also contribute to our current understanding of fluid turbulence in general.

JFM classification

Complex Fluids: Quantum fluids Vortex Flows: Vortex dynamics Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A24
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barenghi, C. F. & Donnelly, R. J. 2009 Vortex rings in classical and quantum systems. Fluid Dyn. Res. 41, 051401.Google Scholar
Barenghi, C. F., Skrbek, L. & Sreenivasan, K. R. 2014 Introduction to quantum turbulence. Proc. Natl Acad. Sci. USA 111, 4647–4652.CrossRefGoogle ScholarPubMed
Borner, H., Schmeling, T. & Schmidt, D. W. 1983 Experiments on the circulation and propagation of large-scale vortex rings in He II. Phys. Fluids 26, 1410–1416.CrossRefGoogle Scholar
Borner, H. & Schmidt, D. W. 1985 Investigation of large-scale vortex rings in He II by acoustic measurements of circulation. In Flow of Real Fluids (ed. Meier, G. E. A. & Obermeier, F.), Lecture Notes in Physics, vol. 235, pp. 135–146. Springer.CrossRefGoogle Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30, 101–116.CrossRefGoogle Scholar
Donnelly, R. J. & Barenghi, C. F. 1998 The observed properties of liquid helium at the saturated vapor pressure. J. Phys. Chem. Ref. Data 27, 1217–1274.CrossRefGoogle Scholar
Duda, D.2017 Quantum turbulence in superfluid helium studied by particle tracking velocimetry visualization technique. PhD thesis, Charles University, Prague, Czech Republic.Google Scholar
Duda, D., La Mantia, M. & Skrbek, L. 2017 Streaming flow due to a quartz tuning fork oscillating in normal and superfluid 4He. Phys. Rev. B 96, 024519.CrossRefGoogle Scholar
Duda, D., Švančara, P., La Mantia, M., Rotter, M. & Skrbek, L. 2015 Visualization of viscous and quantum flows of liquid 4He due to an oscillating cylinder of rectangular cross section. Phys. Rev. B 92, 064519.CrossRefGoogle Scholar
Gan, L. & Nickels, T. B. 2010 An experimental study of turbulent vortex rings during their early development. J. Fluid Mech. 649, 467–496.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Glezer, A. 1988 On the formation of vortex rings. Phys. Fluids 31, 3532–3542.CrossRefGoogle Scholar
Glezer, A. & Coles, D. 1990 An experimental study of a turbulent vortex ring. J. Fluid Mech. 211, 243–283.CrossRefGoogle Scholar
Maxworthy, T. 1974 Turbulent vortex rings. J. Fluid Mech. 64, 227–239.CrossRefGoogle Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81, 465–495.CrossRefGoogle Scholar
Mongiovì, M. S., Jou, D. & Sciacca, M. 2018 Non-equilibrium thermodynamics, heat transport and thermal waves in laminar and turbulent superfluid helium. Phys. Rep. 726, 1–71.Google Scholar
Murakami, M., Hanada, M. & Yamazaki, T. 1987 Flow visualization study on large-scale vortex ring in He II. Jpn. J. Appl. Phys. 26 (Suppl. 26-3), 107–108.CrossRefGoogle Scholar
Sbalzarini, I. F. & Koumoutsakos, P. 2005 Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 151, 182–195.CrossRefGoogle ScholarPubMed
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.CrossRefGoogle Scholar
Stamm, G., Bielert, F., Fiszdon, W. & Piechna, J. 1994a Counterflow-induced macroscopic vortex rings in superfluid helium: visualization and numerical simulation. Physica B 193, 188–194.CrossRefGoogle Scholar
Stamm, G., Bielert, F., Fiszdon, W. & Piechna, J. 1994b On the existence of counterflow induced macroscopic vortex rings in He II. Physica B 194–196, 589–590.CrossRefGoogle Scholar
Sullivan, I. S., Niemela, J. J., Hershberger, R. E., Bolster, D. & Donnelly, R. J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319–347.CrossRefGoogle Scholar
Švančara, P., Hrubcová, P. & La Mantia, M. 2018a Multi-point Lagrangian velocity estimates. In Proceedings of the Conference Topical Problems of Fluid Mechanics 2018 (ed. Šimurda, D. & Bodnár, T.), pp. 281–290. Institute of Thermomechanics of the Academy of Sciences of the Czech Republic.CrossRefGoogle Scholar
Švančara, P., Hrubcová, P., Rotter, M. & La Mantia, M. 2018b Visualization study of thermal counterflow of superfluid helium in the proximity of the heat source by using solid deuterium hydride particles. Phys. Rev. Fluids 3, 114701.CrossRefGoogle Scholar
Švančara, P. & La Mantia, M. 2017 Flows of liquid 4He due to oscillating grids. J. Fluid Mech. 832, 578–599.CrossRefGoogle Scholar
Švančara, P. & La Mantia, M. 2019 Flight-crash events in superfluid turbulence. J. Fluid Mech. 876, R2.CrossRefGoogle Scholar
Van Sciver, S. W. 2012 Helium Cryogenics. Springer.CrossRefGoogle Scholar
Wacks, D. H., Baggaley, A. W. & Barenghi, C. F. 2014 Large-scale superfluid vortex rings at nonzero temperatures. Phys. Rev. B 90, 224514.CrossRefGoogle Scholar