Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-03T00:33:17.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Advective mass transport in two side-by-side liquid microspheres

Published online by Cambridge University Press:  09 June 2020

Qingming Dong  and
Amalendu Sau Open the ORCID record for Amalendu Sau [Opens in a new window]
Qingming Dong
Affiliation:
Department of Aerospace and Software Engineering, Gyeongsang National University, Jinju660701, South Korea
Amalendu Sau*
Affiliation:
Department of Aerospace and Software Engineering, Gyeongsang National University, Jinju660701, South Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

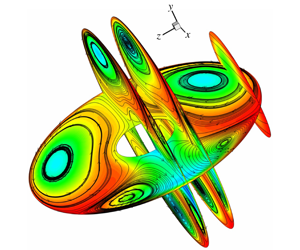
Gaseous $\text{SO}_{2}$ entrainment from a contaminated outer air stream into a pair of side-by-side homogeneous and heterogeneous micro-sized water drops is numerically examined for varied gap ratio $0.1\leqslant G/R\leqslant 6.0$ (ratio of interfacial gap to radius), Reynolds number $20\leqslant Re\leqslant 150$, Weber number $We\leqslant 1.1$, and liquid-phase Péclet number $58.33\leqslant Pe_{l}\leqslant 1055.56$. For $20<Re\leqslant 150$ and $0.1\leqslant G/R\leqslant 6.0$, the separation–attachment induced momentum exchange and imposed non-uniform interfacial shear stress lead to breakup of the primary Hill’s vortex ring and create a significant secondary vortex ring in each drop, which together construct a dominant advective $\text{SO}_{2}$ transport mechanism therein. Beneath a three-dimensional (3-D) topological separation line, the study identifies an active advective mass entrainment process that is led by the ‘inflow’ natured local dynamics of this primary–secondary vortex ring pair. Mechanistically, the secondary and primary vortex rings regulate species transfer into a drop by maintaining the spontaneous inflow-type counter-rotating motion along the 3-D separation line, whereby the $\text{SO}_{2}$ is entrained; and near the attachment points/nodes, two vortices distinctly repulse $\text{SO}_{2}$ entry by virtue of their ‘outflow’ natured local dynamics. The blockage effect and nozzle effect on flow approaching and passing the narrow neck that formed in the presence of a second drop lead to the asymmetric growth of both primary and secondary vortex rings via the locally weakened and enhanced near-interfacial air flow and imposed variable shear stress, which induce the occurrence of an asymmetric mass transfer phenomenon plus biased saturation. The $\text{SO}_{2}$, once entrained, rotates mostly along a spiral orbit of a primary vortex ring, owing to its higher strength. For increased $Re$, the $\text{SO}_{2}$ transport process is reinforced following increased strength of the inflow paired secondary–primary vortex dynamics that enhanced the net entrainment rate and also advanced its transport to the vortex core via augmented convective flow plus radial diffusion. A narrow gap facilitated faster near-gap saturation, while the quantitative $\text{SO}_{2}$ transport rate is decreased by virtue of the produced tapered primary–secondary vortex pairs, associated inner flow bifurcation, and changed topology of the separated wake, which appear similar to what develops for a larger single drop. The gap induced inner vortical structures are characterized by a weaker secondary vortex and a tapered primary vortex near the neck. For heterogeneous drop pairs, the influence of varying 3-D surface flow topology on the two interfaces and the impact of solid fraction $0.1\leqslant S\leqslant 0.8$ ($S=R_{p}/R$, with $R_{p}$ being the radius of the solid core) on the created advective mechanism by the primary–secondary vortex ring pair and resultant $\text{SO}_{2}$ transport are exclusively elucidated.

JFM classification

Drops and Bubbles: Drops and Bubbles
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 897 , 25 August 2020 , A8
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelaal, M. R. & Jog, M. A. 2012 Steady and time-periodic electric field driven enhancement of heat or mass transfer to a drop: internal problem. Intl J. Heat Mass Transfer 55, 251–259.CrossRefGoogle Scholar
Alkislar, M. B., Krothapalli, A. & Butler, G. W. 2007 The effect of streamwise vortices on the aeroacoustics of a Mach 0.9 jet. J. Fluid Mech. 578, 139–169.CrossRefGoogle Scholar
Altwicker, E. R. & Lindhjem, C. E. 1988 Absorption of gases into drops. AIChE J. 34, 329–332.CrossRefGoogle Scholar
Amokrane, H. & Caussade, B. 1999 Gas absorption into a moving spheroidal water drop. J. Atmos. Sci. 56, 1808–1829.2.0.CO;2>CrossRefGoogle Scholar
Angelo, J. B., Lightfoot, E. N. & Howard, D. W. 1966 Generalization of the penetration theory for surface stretch: application and forming and oscillating drops. AIChE J. 12, 751–760.CrossRefGoogle Scholar
Bajer, K. & Moffatt, H. K. 1990 On a class of steady confined Stokes flows with chaotic streamlines. J. Fluid Mech. 212, 337–363.CrossRefGoogle Scholar
Baygents, J. C., Rivette, N. J. & Stone, H. A. 1998 Electrohydrodynamic deformation and interaction of droplet pairs. J. Fluid Mech. 368, 359–375.CrossRefGoogle Scholar
Bhatia, R. & Sirignano, W. A. 1993 Convective burning of a droplet containing a single metal particle. Combust. Flame. 93, 215–229.CrossRefGoogle Scholar
Bryden, M. D. & Brenner, H. 1999 Mass-transfer enhancement via chaotic laminar flow within a droplet. J. Fluid Mech. 379, 319–331.CrossRefGoogle Scholar
Calderbank, P. H. & Korchinski, I. J. O. 1956 Circulation in liquid drops (a heat-transfer study). Chem. Engng Sci. 6, 65–78.CrossRefGoogle Scholar
Cerbino, R., Mazzoni, S., Vailati, A. & Giglio, M. 2005 Scaling behavior for the onset of convection in a colloidal suspension. Phy. Rev. Lett. 94, 064501.CrossRefGoogle Scholar
Chen, W. H. 2001 Unsteady absorption of sulfur dioxide by an atmospheric water droplet with internal circulation. Atmos. Environ. 35, 2375–2393.CrossRefGoogle Scholar
Chen, W. H. & Lu, J. J. 2003 Microphysics of atmospheric carbon dioxide uptake by a cloud droplet containing a solid nucleus. J. Geophys. Res. 108 (D-15), 4470.CrossRefGoogle Scholar
Chiang, C. H., Raju, M. S. & Sirignano, W. A. 1992 Numerical analysis of convecting, vaporizing fuel droplet with variable properties. Intl J. Heat Mass Transfer 35, 1307.CrossRefGoogle Scholar
Chiang, T. P., Sau, A. & Hwang, R. R. 2011 Asymmetry and bifurcations in three-dimensional sudden contraction channel flows. Phys. Rev. E 83, 046313.Google ScholarPubMed
Chiang, C. H. & Sirignano, W. A. 1993 Interacting, convecting, vaporizing fuel droplets with variable properties. Intl J. Heat Mass Transfer 36, 875.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Dandy, D. S. & Leal, L. G. 1989 Buoyancy-driven motion of a deformable drop through a quiescent liquid at intermediate Reynolds numbers. J. Fluid Mech. 208, 161–192.CrossRefGoogle Scholar
Delale, C. F. & Schnerr, G. H. 1996 Transient effects of nucleation in steady and unsteady condensing flows. Intl J. Multiphase Flow 22, 767–781.CrossRefGoogle Scholar
Dong, Q. & Sau, A. 2018 Electrohydrodynamic interaction, deformation, and coalescence of suspended drop pairs at varied angle of incidence. Phys. Rev. Fluids 3, 073701.CrossRefGoogle Scholar
Dong, Q. & Sau, A. 2019 Breakup of a leaky dielectric drop in a uniform electric field. Phys Rev. E 99, 043106.Google Scholar
Elperin, T., Fominykh, A. & Krasovitov, B. 2009 Effect of altitude concentration gradient of soluble gaseous pollutants on their scavenging by falling rain droplets. J. Atmos. Sci. 66, 2349–2358.CrossRefGoogle Scholar
Elperin, T., Fominykh, A., Krasovitov, B. & Lushnikov, A. 2013 Isothermal absorption of soluble gases by atmospheric nanoaerosols. Phys. Rev. E 87, 012807.Google ScholarPubMed
Garner, F. H. & Lane, J .J. 1959 Mass transfer to drops of liquid suspended in a gas stream. II: Experimental work and results. Trans. Inst. Chem. Engrs 37, 162–172.Google Scholar
Girard, F., Antoni, M., Faure, S. & Steinchen, A. 2006 Evaporation and Marangoni driven convection in small heated water droplets. Langmuir 22, 11085–11091.CrossRefGoogle ScholarPubMed
Grassia, P. & Ubal, S. 2018 Streamline-averaged mass transfer in a circulating drop. Chem. Engng Sci. 190, 190–218.CrossRefGoogle Scholar
Gunther, A., Jhunjhunwala, M. & Thalmann, M. 2005 Micromixing of miscible liquids in segmented gas–liquid flow. Langumir 21, 1547–1555.CrossRefGoogle ScholarPubMed
Hadamard, J .S. 1911 Mouvement permanent lent d’une sphere liquide et visqueuse dans un liquide visqueux. C. R. Acad. Sci. Paris 152, 1735–1738.Google Scholar
Hamielec, A. E. & Johnson, A. I. 1962 Viscous flow around fluid spheres at intermediate Reynolds numbers. Can. J. Chem. Engng 40, 41–45.CrossRefGoogle Scholar
Handlos, A. E. & Baron, T. 1957 Mass and heat transfer from drops in liquid–liquid extraction. AIChE J. 3, 127–136.CrossRefGoogle Scholar
Hsiang, L. P. & Faeth, G. M. 1992 Near-limit drop deformation and secondary breakup. Int. J. Multiphase Flow 18, 635–652.CrossRefGoogle Scholar
Hunt, J. C. R., Abell, C. J., Peterka, J. A. & Woo, H. 1978 Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J. Fluid Mech. 86, 179–200.CrossRefGoogle Scholar
Jahne, B. & Haubecker, H. 1998 Air-water gas exchange. Annu. Rev. Fluid Mech. 30, 443–468.CrossRefGoogle Scholar
Jana, S. C. & Ottino, J. M. 1992 Chaos-enhanced transport in cellular flows. Phil. Trans. R. Soc. Lond. A 338, 519–532.Google Scholar
Johnson, D. & Narayanan, R. 1999 A tutorial on the Rayleigh–Marangoni–Benard problem with multiple layers and side wall effects. Chaos 9, 124–140.CrossRefGoogle ScholarPubMed
Kaji, R., Hishinuma, Y. & Kuroda, H. 1985 SO2 absorption by water droplets. J. Chem. Engng Japan. 18, 169–172.CrossRefGoogle Scholar
Kaneda, M., Hyakuta, K., Takao, Y., Ishizuka, H. & Fukai, J. 2008 Internal flow in polymer solution droplets deposited on a lyophobic surface during a receding process. Langmuir 24, 9102–9109.CrossRefGoogle ScholarPubMed
Kim, I., Elghobashi, S. & Sirignano, W. A. 1993 Three-dimensional flow over two spheres placed side by side. J. Fluid Mech. 246, 465–488.CrossRefGoogle Scholar
Kinoshita, H., Kaneda, S., Fujii, T. & Oshima, M. 2007 Three-dimensional measurement and visualization of internal flow of a moving droplet using confocal micro-PIV. Lab Chip 7, 338–346.CrossRefGoogle ScholarPubMed
Krishnamurthy, S., Bhattacharya, P. & Phelan, P. E. 2006 Enhanced mass transport in nanofluids. Nano. Lett. 6, 419–423.CrossRefGoogle ScholarPubMed
Kronig, R. & Brink, J. C. 1950 On the theory of extraction from falling droplets. Appl. Sci. Res. A2, 142–154.Google Scholar
Leclair, B. P., Hamielec, A. E., Pruppacher, H. R. & Hall, W. D. 1972 A theoretical and experimental study of the internal circulation in water drops falling at terminal velocity in air. J. Atmos. Sci. 29, 728–740.2.0.CO;2>CrossRefGoogle Scholar
Legendre, R. 1956 Séparation de l’écoulement luminaire tridimensionnel. Rech. Aérosp. 105, 3–8.Google Scholar
Li, Y., Jain, M., Ma, Y. & Nandakumar, K. 2015 Control of the breakup process of viscous droplets by an external electric field inside a microfluidic device. Soft Matt. 11, 3884–3899.CrossRefGoogle ScholarPubMed
Lighthill, M. J. 1963 Attachment and Separation in 3D Flows (ed. Rosenhead, L.), Laminar Boundary Layers. Oxford University Press.Google Scholar
Mandal, D. K. & Bakshi, S. 2012 Internal circulation in a single droplet evaporating in a closed chamber. Intl J. Multiphase Flow 42, 42–51.CrossRefGoogle Scholar
Maskell, E. C.1955 Flow separation in three dimensions. Technical Report RAE Aero Rept. 2565.Google Scholar
Ogata, J. & Yabe, A. 1993 Augmentation of boiling heat transfer by utilizing the EHD effect-EHD behavior of boiling bubbles and heat transfer characteristics. Intl J. Heat Mass Transfer 36, 783–791.CrossRefGoogle Scholar
Oliver, D. L. R. & Chung, J. N. 1986 Conjugate unsteady hear transfer from a spherical droplet at low Reynolds number. Intl J. Heat Mass Transfer 29, 879–887.CrossRefGoogle Scholar
Patankar, S. V. 1980 Numerical Heat Transfer and Fluid Flow. Hemisphere.Google Scholar
Peng, Y. F., Mittal, R., Sau, A. & Hwang, R. R. 2010 Nested Cartesian grid method for viscous incompressible flows. J. Comput. Phys. 229, 7072–7101.CrossRefGoogle Scholar
Peng, Y. F., Sau, A., Hwang, R. R., Yang, W. C. & Hsieh, C. M. 2012 Criticality of flow transition behind two side-by-side elliptic cylinders. Phys. Fluids 24, 034102.CrossRefGoogle Scholar
Peng, Y. F. & Sau, A. 2015 Transitional hysteresis loop and coexistence of synchronized shedding in coupled wakes. Phys. Fluids 27, 074104.CrossRefGoogle Scholar
Pompano, R. R., Liu, W., Du, W. & Ismagilov, R. F. 2011 Microfluidics Using spatially defined arrays of droplets in one, two, and three dimensions. Annu. Rev. Anal. Chem 4, 59–81.CrossRefGoogle ScholarPubMed
Prasher, R. 2005 Thermal conductivity of nanoscale colloidal solutions (Nanofluids). Phy. Rev. Lett. 94, 025901.CrossRefGoogle Scholar
Rivkind, V. Y. & Ryskin, G. 1976 Flow structure in motion of a spherical drop in a fluid medium at intermediate Reynolds numbers. Fluid Dyn. 11, 5–12.CrossRefGoogle Scholar
Raju, M. S. & Sirignano, W. A. 1990 Interaction between two vaporizing droplets in an intermediate Reynolds number flow. Phys. Fluids. A2, 1780–1796.CrossRefGoogle Scholar
Sau, A. 2002 Vortex dynamics and mass entrainment in a rectangular channel with a suddenly expanded and contracted part. Phys. Fluids 14, 3280.CrossRefGoogle Scholar
Sau, A. 2004 Generation of streamwise vortices in square sudden-expansion flows. Phys. Rev. E 69, 056307.Google ScholarPubMed
Sau, A. 2011 Role of streamwise dynamics in spreading and mixing of flows through a rectangular sudden expansion. Phys. Fluids 23, 083602.CrossRefGoogle Scholar
Sirignano, W. A. 1983 Fuel droplet vaporization and spray combustion theory. Prog. Energy Combust. Sci. 9, 291–322.CrossRefGoogle Scholar
Sirignano, W. A. 1999 Fluid Dynamics and Transport of Droplets and Sprays. Cambridge University Press.CrossRefGoogle Scholar
Stone, H. A., Nadim, A. & Strogatz, S. H. 1991 Chaotic streamlines inside drops immersed in steady Stokes flows. J. Fluid Mech. 232, 629–646.CrossRefGoogle Scholar
Stroock, A. D., Dertinger, S. K. W., Ajdari, A., Mezic, I., Stone, H. A. & Whitesides, G. M. 2002 Chaotic mixer for microchannels. Science 295, 647–651.CrossRefGoogle ScholarPubMed
Sundararajan, T. & Ayyaswamy, P. S. 1984 Hydrodynamics and heat transfer associated with condensation on a moving drop: solutions for intermediate Reynolds numbers. J. Fluid Mech. 149, 33–58.CrossRefGoogle Scholar
Tal, R., Lee, D. N. & Sirignano, W. A. 1983 Hydrodynamics and heat transfer in sphere assemblages-cylindrical cell models. Intl J. Heat Mass Transfer 26, 1265–1273.Google Scholar
Tice, J. D., Song, H., Lyon, A. D. & Ismagilov, R. F. 2003 Formation of droplets and mixing in multiphase microfluidics at low values of the Reynolds and the capillary numbers. Langmuir 19, 9127–9133.CrossRefGoogle Scholar
Ubal, S., Harrison, C. H., Grassia, P. & Korchinsky, W. J. 2010 Numerical simulation of mass transfer in circulating drops. Chem. Engng Sci. 65, 2934–2956.CrossRefGoogle Scholar
Vigo, C. R. & Ristenpart, D. D. 2010 Aggregation and coalescence of oil droplets in water via electrohydrodynamic flows. Langmuir 26, 10703–10707.CrossRefGoogle ScholarPubMed
Watada, H., Hamielec, A. E. & Johnson, A. I. 1970 A theoretical study of mass transfer with chemical reaction in drops. Can. J. Chem. Engng 48, 255–261.CrossRefGoogle Scholar
Wong, S. C. & Lin, A. C. 1992 Internal temperature distributions of droplets vaporizing in high-temperature convective flows. J. Fluid Mech. 237, 671–687.CrossRefGoogle Scholar
Wu, G. & Sirignano, W. A. 2011a Transient convective burning of fuel droplets in single-layer arrays. Combust. Theor. Model. 15, 227–243.CrossRefGoogle Scholar
Wu, G. & Sirignano, W. A. 2011b Transient convective burning of fuel droplets in double-layer arrays. Combust. Flame 158, 2395–2407.CrossRefGoogle Scholar
Wu, G. & Sirignano, W. A. 2011c Transient convective burning of a periodic fuel droplet array. Proc. Combust. Inst. 33, 2109–2116.CrossRefGoogle Scholar
Wylock, C., Colinet, P. & Haut, B. 2012 Gas absorption into a spherical liquid droplet: numerical and theoretical study. Chem. Engng J 207–208, 851–864.CrossRefGoogle Scholar
Xie, J. W., Lim, L. K., Phua, Y. Y., Hua, J. S. & Wang, C. H. 2006 Electrohydrodynamic atomization for biodegradable polymeric particle production. J. Colloid Interface Sci. 302, 103–112.CrossRefGoogle ScholarPubMed
Yoshitake, Y., Yasumatsu, S., Nakaso, K. & Fukai, J. 2010 Structure of circulation flows in polymer solution droplets receding on flat surfaces. Langmuir 26, 3923–3928.CrossRefGoogle ScholarPubMed
Zaman, K. B. M. Q. 1996 Axis switching and spreading of an asymmetric jet: the role of coherent structure dynamics. J. Fluid Mech. 316, 1–27.CrossRefGoogle Scholar