Added mass energy recovery of octopus-inspired shape change

Abstract

Dynamic shape change of the octopus mantle during fast jet escape manoeuvres results in added mass energy recovery to the energetic advantage of the octopus, giving escape thrust and speed additional to that due to jetting alone. We show through numerical simulations and experimental validation of overall wake behaviour, that the success of the energy recovery is highly dependent on shrinking speed and Reynolds number, with secondary dependence on shape considerations and shrinking amplitude. 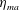The added mass energy recovery ratio $\unicode[STIX]{x1D702}_{ma}$, which measures momentum recovery in relation to the maximum momentum recovery possible in an ideal flow, increases with increasing the non-dimensional shrinking parameter 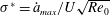$\unicode[STIX]{x1D70E}^{\ast }={\dot{a}}_{max}/U\sqrt{\mathit{Re }_{0}}$, where 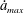${\dot{a}}_{max}$ is the maximum shrinking speed, 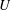$U$ is the characteristic flow velocity and 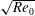$\sqrt{\mathit{Re }_{0}}$ is the Reynolds number at the beginning of the shrinking motion. An estimated threshold 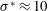$\unicode[STIX]{x1D70E}^{\ast }\approx 10$ determines whether or not enough energy is recovered to the body to produce net thrust. Since there is a region of high transition for 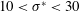$10<\unicode[STIX]{x1D70E}^{\ast }<30$ where the recovery performance varies widely and for $\unicode[STIX]{x1D70E}^{\ast }>100$ added mass energy is recovered at diminishing returns, we propose a design criterion for shrinking bodies to be in the range of 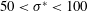$50<\unicode[STIX]{x1D70E}^{\ast }<100$, resulting in 61–82 % energy recovery.