Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-28T20:38:25.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Active volume of water in a laboratory aquifer

Published online by Cambridge University Press:  27 January 2025

E. Lajeunesse Open the ORCID record for E. Lajeunesse [Opens in a new window] ,
O. Devauchelle Open the ORCID record for O. Devauchelle [Opens in a new window] ,
J. Douçot  and
V. Jules Open the ORCID record for V. Jules [Opens in a new window]
E. Lajeunesse*
Affiliation:
Université Paris Cité, Institut de Physique du Globe de Paris, CNRS, F-75005 Paris, France
O. Devauchelle
Affiliation:
Université Paris Cité, Institut de Physique du Globe de Paris, CNRS, F-75005 Paris, France
J. Douçot
Affiliation:
CY Cergy Paris Université, Laboratoire Géosciences et Environnement Cergy (GEC), 1, rue Descartes, 95000 Neuville-sur-Oise, France
V. Jules
Affiliation:
Institut Pprime, CNRS-Université de Poitiers-ISAE ENSMA, TSA 51124, 86073 Poitiers Cedex 9, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

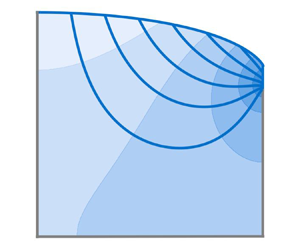
During a rainfall event, water infiltrates into the ground where it accumulates in porous rocks. This accumulation pushes the underlying groundwater towards neighbouring streams, where it runs to the sea. After the rain has stopped, the aquifer gradually releases its excess water, as the water table relaxes, until the next rain. In the absence of recharge, the water table would eventually reach its horizontal equilibrium position. The volume of groundwater stored above this level, which we call the active volume, sustains the river between two rainfall events. In this article, we use an experimental aquifer recharged by artificial rain to investigate how this active volume depends on the rainfall rate. Restricting our analysis to the steady-state regime, wherein the discharge into the stream balances rainfall, we explore a broad range of rainfall rates, for which the water table deforms significantly. We find that the active volume of water stored in the aquifer decreases with its depth. Using conformal mapping, we derive the flow equations and develop a numerical procedure that accounts for the active volume of groundwater in our experiments. In the case of an infinitely deep aquifer, the problem admits a closed-form solution, which provides a satisfying estimate of the active volume when the aquifer's depth is at least half its width. In the general case, a rougher estimate results from the energy balance of the dissipative groundwater flow.

JFM classification

Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1002 , 10 January 2025 , A36
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aigler, B.V. & Ge, S. 2013 Evaluation of groundwater withdrawal from a mountain watershed, Colorado, USA. Environ. Earth Sci. 69, 1901–1913.CrossRefGoogle Scholar
Alley, W.M., Healy, R.W., LaBaugh, J.W. & Reilly, T.E. 2002 Flow and storage in groundwater systems. Science 296 (5575), 1985–1990.CrossRefGoogle ScholarPubMed
Andreotti, B., Forterre, Y. & Pouliquen, O. 2013 Granular Media: Between Fluid and Solid. Cambridge University Press.CrossRefGoogle Scholar
Bear, J. 2018 Modeling Phenomena of Flow and Transport in Porous Media. Springer.CrossRefGoogle Scholar
Benettin, P., Kirchner, J.W., Rinaldo, A. & Botter, G. 2015 Modeling chloride transport using travel time distributions at Plynlimon, Wales. Water Resour. Res. 51 (5), 3259–3276.CrossRefGoogle Scholar
Bierman, P.R. & Montgomery, D.R. 2014 Key Concepts in Geomorphology. W.H. Freeman and Company.Google Scholar
Boussinesq, J. 1903 Sur un mode simple d’écoulement des nappes d'eau d'infiltration à lit horizontal, avec rebord vertical tout autour lorsqu'une partie de ce rebord est enlevée depuis la surface jusqu'au fond. C. R. Acad. Sci. 137 (5), 11.Google Scholar
Brutsaert, W. & Nieber, J.L. 1977 Regionalized drought flow hydrographs from a mature glaciated plateau. Water Resour. Res. 13 (3), 637–643.CrossRefGoogle Scholar
Carman, P.C. 1937 Fluid flow through a granular bed. Transactions of the Institution of Chemical Engineers, vol. 15, pp. 150–156.Google Scholar
Costigan, K.H., Kennard, M.J., Leigh, C., Sauquet, E., Datry, T. & Boulton, A.J. 2017 Flow regimes in intermittent rivers and ephemeral streams. In Intermittent Rivers and Ephemeral Streams (ed. T. Datry, N. Bonada & A. Boulton), pp. 51–78. Academic Press.CrossRefGoogle Scholar
De Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.CrossRefGoogle Scholar
Devauchelle, O., Petroff, A.P., Lobkovsky, A.E. & Rothman, D.H. 2011 Longitudinal profile of channels cut by springs. J. Fluid Mech. 667 (1), 38–47.CrossRefGoogle Scholar
Devauchelle, O., Petroff, A.P., Seybold, H.F. & Rothman, D.H. 2012 Ramification of stream networks. Proc. Natl Acad. Sci. USA 109 (51), 20832–20836.CrossRefGoogle ScholarPubMed
Dunne, T. 1990 Hydrology, mechanics, and geomorphic implications of erosion by subsurface flow. In Groundwater Geomorphology: The Role of Subsurface Water in Earth-Surface Processes and Landforms (ed. C.G. Higgins & D.R. Coates), Geological Society of America Special Paper. vol. 252, pp. 1–28.Google Scholar
Dupuit, J. 1863 Études théoriques et pratiques sur le mouvement des eaux dans les canaux découverts et à travers les terrains perméables. Dunod.Google Scholar
Guérin, A., Devauchelle, O. & Lajeunesse, E. 2014 Response of a laboratory aquifer to rainfall. J. Fluid Mech. 759, R1.CrossRefGoogle Scholar
Guérin, A., Devauchelle, O., Robert, V., Kitou, T., Dessert, C., Quiquerez, A., Allemand, P. & Lajeunesse, E. 2019 Stream-discharge surges generated by groundwater flow. Geophys. Res. Lett. 46 (13), 7447–7455.CrossRefGoogle Scholar
Haria, A.H. & Shand, P. 2004 Evidence for deep sub-surface flow routing in forested upland Wales: implications for contaminant transport and stream flow generation. Hydrol. Earth Syst. Sci. Discuss. 8 (3), 334–344.CrossRefGoogle Scholar
Harrold, L.L. 1934 Relation of stream-flow to ground-water levels. EOS Trans. AGU 15 (2), 414–416.Google Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Maths 20 (3–4), 251–266.Google Scholar
Hecht, F., Pironneau, O., Le Hyaric, A. & Ohtsuka, K. 2005 FreeFem++ Manual. Laboratoire Jacques Louis Lions.Google Scholar
Horton, R.E. 1936 Maximum ground-water levels. EOS Trans. AGU 17 (2), 344–357.Google Scholar
Jules, V. 2020 Écoulement dans un aquifère non confiné profond alimenté par la pluie. PhD thesis, Université Paris Cité.Google Scholar
Jules, V., Lajeunesse, E., Devauchelle, O., Guérin, A., Jaupart, C. & Lagrée, P.-Y. 2021 Flow and residence time in a two-dimensional aquifer recharged by rainfall. J. Fluid Mech. 917, A13.CrossRefGoogle Scholar
Lehr, J.H. 1963 Groundwater: flow toward an effluent stream. Science 140 (3573), 1318–1320.CrossRefGoogle ScholarPubMed
Leverett, M.C. 1941 Capillary behavior in porous solids. Trans. AIME 142 (1), 152–169.CrossRefGoogle Scholar
Pasquet, S., Marçais, J., Hayes, J.L., Sak, P.B., Ma, L. & Gaillardet, J. 2022 Catchment-scale architecture of the deep critical zone revealed by seismic imaging. Geophys. Res. Lett. 49 (13), e2022GL098433.CrossRefGoogle Scholar
Pauwels, V.R.N. & Troch, P.A. 2010 Estimation of aquifer lower layer hydraulic conductivity values through base flow hydrograph rising limb analysis. Water Resour. Res. 46 (3).CrossRefGoogle Scholar
Petroff, A.P., Devauchelle, O., Abrams, D.M., Lobkovsky, A.E., Kudrolli, A. & Rothman, D.H. 2011 Geometry of valley growth. J. Fluid Mech. 673 (245–254), 6.CrossRefGoogle Scholar
Petroff, A.P., Devauchelle, O., Kudrolli, A. & Rothman, D.H. 2012 Four remarks on the growth of channel networks. C. R. Geosci. 344 (1), 33–40.CrossRefGoogle Scholar
Pokhrel, Y., et al. 2021 Global terrestrial water storage and drought severity under climate change. Nat. Clim. Chang. 11 (3), 226–233.CrossRefGoogle Scholar
Polubarinova-Kochina, P.Y. 1962 Theory of Ground Water Movement. Princeton University Press.Google Scholar
Shercliff, J.A. 1975 Seepage flow in unconfined aquifers. J. Fluid Mech. 71 (1), 181–192.CrossRefGoogle Scholar
Taylor, R.G., et al. 2013 Ground water and climate change. Nat. Clim. Chang. 3 (4), 322–329.CrossRefGoogle Scholar
Toth, J. 1963 A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 68 (16), 4795–4812.CrossRefGoogle Scholar
Troch, P.A., et al. 2013 The importance of hydraulic groundwater theory in catchment hydrology: the legacy of Wilfried Brutsaert and Jean-Yves Parlange. Water Resour. Res. 49 (9), 5099–5116.CrossRefGoogle Scholar
Tschapek, M., Falasca, S. & Wasowski, C. 1985 The undrainable water in quartz sand and glass beads. Powder Technol. 42 (2), 175–180.CrossRefGoogle Scholar
Zhukovsky, N.E. 1932 Seepage of water through dams. Poln. Sobr. Soch. 7, 323–363.Google Scholar