Article contents
The Optimal Level of Forward Exchange Transactions
Published online by Cambridge University Press: 19 October 2009
Extract
The basic model of this paper is that of a transactor who is to receive at a specified time t in the future a fixed quantity of domestic funds Ad and a fixed quantity of foreign funds Af. It is further assumed that there exists a forward market in foreign exchange in which one unit of foreign currency can be bought and sold at a given and known forward rate rf, the domestic currency price of one unit of foreign currency. Let X be the net forward purchases of foreign exchange that the transactor undertakes at the market rate rf; a negative value of X indicates net sales of forward exchange. It is assumed that at time t the foreign currency will be convertible for the transactor at a fixed but unknown spot exchange rate 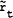 and that the transactor can assess or derive a probability distribution on this spot exchange rate f(rt) for rt > 0. Finally, it is assumed that the transactor can express a utility function u on the domestic currency equivalent of his ending currency holdings. This paper considers the problem of determining the optimal level of forward exchange purchases X0.
and that the transactor can assess or derive a probability distribution on this spot exchange rate f(rt) for rt > 0. Finally, it is assumed that the transactor can express a utility function u on the domestic currency equivalent of his ending currency holdings. This paper considers the problem of determining the optimal level of forward exchange purchases X0.
- Type
- Research Article
- Information
- Copyright
- Copyright © School of Business Administration, University of Washington 1973
References
- 3
- Cited by


