Article contents
Note on “Optimal Growth Portfolios When Yields are Serially Correlated”
Published online by Cambridge University Press: 19 October 2009
Extract
In [2] Hakansson and Liu presented a multiperiod portfolio model in which there is an optimal myopic policy. In particular, at any decision point j and state m the optimal amount to invest in opportunity i, namely 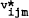 , may be found by maximizing
, may be found by maximizing
(42a) 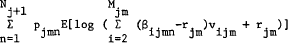
subject to
(42b) 
(42c) 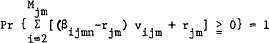 ,
,
where the expectation is taken with respect to the β's, and the p's and r are positive constants (r > 1). Assumptions are made in [2] which guarantee that (42) has a unique optimal solution and that the set of vijm which satisfies (42b and 42c) is a nonempty, compact, convex set for all j and m.
- Type
- Communications
- Information
- Journal of Financial and Quantitative Analysis , Volume 7 , Issue 4 , September 1972 , pp. 1995 - 2000
- Copyright
- Copyright © School of Business Administration, University of Washington 1972
References
- 13
- Cited by


