Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T07:48:51.028Z Has data issue: false hasContentIssue false
  • English
  • Français

Deposit Variability and Bank Size

Published online by Cambridge University Press:  19 October 2009

George G. Kaufman
Get access Rights & Permissions [Opens in a new window]

Extract

A number of recent articles have explored the reasons underlying observed differences in deposit variability among commercial banks. The variability of deposits at individual banks is of interest to bank management, the Federal Reserve, and the general public for several reasons:

1. Deposit variability is frequently included as an important determinant of portfolio strategy. The more volatile a bank's deposits are, the more liquid its mix of assets will be.

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , Volume 7 , Issue 5 , December 1972 , pp. 2087 - 2096
Copyright
Copyright © School of Business Administration, University of Washington 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 For example: Chairnoff, Hugh, “Deposit Variability: A Banker's Headache,” Business Review. (Federal Reserve Bank of Philadelphia, September 1967), pp. 9–15Google Scholar; Gramley, Lyle E., “Deposit Instability at Individual Banks” in Essays on Commercial Banking (Federal Reserve Bank of Kansas City, 1962), pp. 41–53Google Scholar; Murphy, Neil B., “A Cross-Section Analysis of Demand Deposit Variability,” Journal of Financial and Quantitative Analysis, vol. 3 (March 1968), pp. 87–95Google Scholar; Rangarajan, C., “Deposit Variability in Individual Banks,” National Banking Review, vol. 4 (September 1966), pp. 61–71Google Scholar; Struble, Frederick M. and Wilkerson, Carrol H., “Bank Size and Deposit Variability,” Monthly Review (Federal Reserve Bank of Kansas City, November–December 1967), pp. 3–9.Google Scholar

2 Kane, Edward E. and Malkiel, Burton G., “Bank Portfolio Allocation, Deposit Variability and the Availability Doctrine,” Quarterly Journal of Economics, vol. 79 (February 1965), pp. 113–134Google Scholar; Hester, Donald D., “An Empirical Examination of a Commercial Bank Loan Offer Function,” Yale Economic Essays, vol. 2 (Spring 1962), pp. 3–57.Google Scholar

3 Bernard, Shull, “Report on Research Undertaken in Connection with a System Study,” Reappraisal of the Federal Reserve Discount Mechanism (U.S. Board of Governors of the Federal Reserve System, 1968), p. 35.Google Scholar

4 shull, “Report on Research,”pp. 22–35. Kane and Malkiel, “Bank Portfolio Allocation,” p. 120; Dewald, William G. and Dreese, G. Richard, “Bank Behavior with Respect to Deposit Variability,” Journal of Finance, vol. 25 (September 1970), pp. 869–879.CrossRefGoogle Scholar

5 Dewald and Dreese, “Bank Behavior,” pp. 875–879.

6 Robinson, Roland, The Management of Bank Funds (New York: McGraw-Hill, 1962), pp. 88–89Google Scholar; Gramley, “Deposit Instability,” p. 43.

7 In the sample of banks developed for this study, demand deposits due to banks and demand deposits of the U.S. Government accounted for about 0 percent and 0.5 percent, respectively, of total deposits at banks with deposits of less than $5 million and about 5.5 percent and 1.3 percent, respectively, of deposits at banks with deposits in excess of $100 million.

8 Dewald and Dreese, “Bank Behavior,” p. 872; Struble and Wilkerson, “Bank Size,” pp. 6–9; Chairnoff, “Deposit Variability,” pp. 10–15. Differences in variability in different categories of deposits are evident from the data below for all 53 large member commercial banks which in 1969 reported balance sheet information weekly to the Federal Reserve Bank of Chicago. The data are described in greater detail later in the study.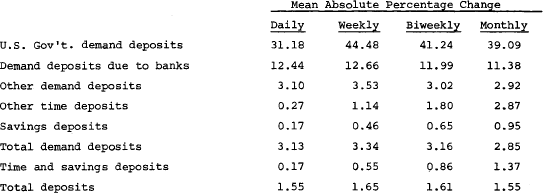

9 Gramley, “Deposit Instability,” p. 43.

10 Robinson, Management, p. 89.

11 The major exception to the finding is Murphy, who fails to find a significant relationship between bank size and deposit variability. But since deposit mix, which is related to bank size, is also specified in his model, part of the overall size impact is drained.

12 Shull, “Report,” pp. 22–35.

13 The coefficient of variation is used by Chairnoff and Rangarajan. Murphy and Dewald and Dreese use the ratio of the standard error of the estimate to the mean. In their recent article, Dewald and Dreese also take issue with the appropriateness of previous attempts to measure deposit variability, but for different reasons than presented here. They argue that bank asset strategy is related not to overall deposit variability but only to that part of the variability that cannot be predicted. Thus, they consider the standard error of the estimate a better measure. While Murphy also uses the standard error of the estimate, he adjusts only for trend; Dewald and Dreese adjust also for seasonality. They show that such a measure explains certain short-term bank reserve adjustments better than the coefficient of variation. It does not necessarily follow, however, that bank total asset management is also more strongly affected by unpredictable deposit variability than total variability. Given positive transactions costs, it appears reasonable that banks consider both predictable and unpredictable variability in determining their asset mix, although the elasticities of the two may differ. Unfortunately, no direct evidence on this question or on the relationship between bank size and variability can be obtained from the information published in the Dewald and Dreese article.

14 To the extent total deposits constrain total assets, a bank would need to adjust its asset portfolio in every one of the eight periods under distribution 1 but only once, after the fourth period, under Distribution 2.

15 Johnston observes that the reliability of the variance of a series decreases as the autocorrelation in the series increases. Johnston, J., Econometric Methods (New York, N.Y.: McGraw-Hill Book Company, 1963), pp. 179–199.Google Scholar

Unlike the CV, the MAPC is sensitive to the value of the initial observation, varying inversely with it. This bias is relatively unimportant if the number of observations is great. Also, it can be eliminated altogether by using the geometric MAPC. Alternatively, reliable variance statistics can be computed from first differences or similar transformations of the autocorrelated series.

16 Dewald and Dreese use daily observations but, as noted earlier, do not investigate directly the relationship between bank size and deposit variability.

17 Variability was calculated by the following equations: Daily: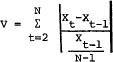 Weekly, biweekly, and monthly: 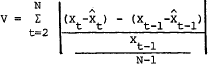where: X is the dollar amount of deposits in period t, N is the total number of periods t, and ◯ is the trend value of deposits.

18 The relatively low values of the simple correlation coefficients suggest that many forces besides bank size affect the variability of deposits at individual banks. Some of these other forces are identified in the studies cited in footnote 1.

19 Correlation coefficients were computed only for banks with nonzero deposits in the particular category.

20 Similar results were obtained using nontrend adjusted data. The same pattern was also observed, but less clearly, when deposit variability was measured by the coefficient of variation.