Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T15:09:35.438Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability Theorems for Solutions to the Optimal Inventory Equation

Published online by Cambridge University Press:  14 July 2016

S. Edward Boylan
S. Edward Boylan*
Affiliation:
Rutgers, The State University, Newark, N.J.
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous paper, [1] it was shown that a solution, f(x) will exist for the optimal inventory equation 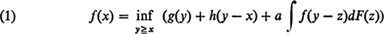(where f(y − z) = f(0), y < z) provided:

  1. 1. g(x) ≧ 0, x ≧ 0;

  2. 2. 0 < a < 1;

  3. 3. h(x) is monotonically nondecreasing, h(0) = 0;

  4. 4. F is a distribution function on [0, ∞);

    (In [1], 1–4 were denoted collectively as (A).)

    and either

  5. 5a. g(x) is continuous for all x ≧ 0;

  6. 5b. limx→∞g(x) = ∞;

  7. 5c h(x) is continuous for all x > 0 (Theorem 2 of [1]);

    or

  8. 6. g(x) is uniformly continuous for all x ≧ 0 (Theorem 3 of [1]).

Type
Short Communications
Information
Journal of Applied Probability , Volume 6 , Issue 1 , April 1969 , pp. 211 - 217
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Boylan, E. (1966) Existence and uniqueness theorems for the optimal inventory equation. SIAM J. Appl. Math. 14, 961–969.Google Scholar
[2] Feller, W. (1966) An Introduction to Probability Theory and its Applications Vol. II. Wiley, New York.Google Scholar
[3] Rudin, W. (1964) Principles of Mathematical Analysis. McGraw Hill, New York. 2nd edition.Google Scholar
[4] Bellman, R. (1957) Dynamic Programming. Princeton University Press, Princeton, N. J. Google Scholar