Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-17T13:38:53.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Some conditional properties of superprocesses in random environments

Part of: Stochastic processes Markov processes

Published online by Cambridge University Press:  08 April 2025

Jiawei Liu Open the ORCID record for Jiawei Liu [Opens in a new window] ,
Shuxiong Zhang Open the ORCID record for Shuxiong Zhang [Opens in a new window]  and
Jie Xiong
Jiawei Liu*
Affiliation:
Jiangxi Normal University
Shuxiong Zhang*
Affiliation:
Anhui Normal University
Jie Xiong*
Affiliation:
Southern University of Science and Technology
*
*Postal address: School of Mathematics and Statistics, Jiangxi Normal University, Nanchang, China. Email: jwliu@mail.bnu.edu.cn
**Postal address: School of Mathematics and Statistics, Anhui Normal University, Wuhu, China. Email: shuxiong.zhang@mail.bnu.edu.cn
***Postal address: Department of Mathematics and SUSTech International Center for Mathematics, Southern University of Science and Technology, Shenzhen, China. Email: xiongj@sustech.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a superprocess 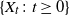$\{X_t\colon t\geq 0\}$ in a random environment described by a Gaussian field 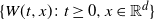$\{W(t,x)\colon t\geq 0,x\in \mathbb{R}^d\}$. First, we set up a representation of 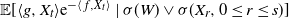$\mathbb{E}[\langle g, X_t\rangle\mathrm{e}^{-\langle \,f,X_t\rangle }\mid\sigma(W)\vee\sigma(X_r,0\leq r\leq s)]$ for 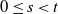$0\leq s < t$ and some functions f,g, which generalizes the result in Mytnik and Xiong (2007, Theorem 2.15). Next, we give a uniform upper bound for the conditional log-Laplace equation with unbounded initial values. We then use this to establish the corresponding conditional entrance law. Finally, the excursion representation of 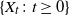$\{X_t\colon t\geq 0\}$ is given.

Keywords

Entrance lawexcursion representationstochastic log-Laplace equation

MSC classification

Primary: 60G57: Random measures 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60J35: Transition functions, generators and resolvents
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Dawson, D. A. and Li, Z. (2003). Construction of immigration superprocesses with dependent spatial motion from one-dimensional excursions. Prob. Theory Relat. Fields 127, 37–61.CrossRefGoogle Scholar
Dynkin, E. B. (1989). Three classes of infinite dimensional diffusion processes. J. Funct. Anal. 86, 75–110.CrossRefGoogle Scholar
Eckhoff, M., Kyprianou, A. E. and Winkel, M. (2015). Spines, skeletons and the strong law of large numbers for superdiffusions. Ann. Prob. 43, 2545–2610.CrossRefGoogle Scholar
Getoor, R. K. and Glover, J. (1987). Constructing Markov processes with random times of birth and death. In Seminar on Stochastic Processes, eds E. Cinlar et al. Birkhauser, Boston, MA.CrossRefGoogle Scholar
Hu, Y., Nualart, D. and Song, J. (2013). A nonlinear stochastic heat equation: Hölder continuity and smoothness of the density of the solution. Stoch. Process. Appl. 123, 1083–1103.CrossRefGoogle Scholar
Itô, L. (1970). Poisson point processes attached to Markov processes. In Proc. Sixth Berkeley Symp. Math. Stat. Prob. Vol. 3, pp. 225–239.Google Scholar
Kallianpur, G. (1980). Stochastic Filtering Theory. Springer, Berlin.CrossRefGoogle Scholar
Kallianpur, G. and Xiong, J. (1995). Stochastic Differential Equations in Infinite Dimensional Spaces (IMS Lect. Notes Monograph Ser. 26). Institute of Mathematical Statistics.Google Scholar
Kotelenez, P. (1992). Comparison methods for a class of function valued stochastic partial differential equations. Prob. Theory Relat. Fields 93, 1–19.Google Scholar
Kuznetsov, S. E. (1974). Construction of Markov processes with random times of birth and death. Theory Prob. Appl. 18, 571–575.CrossRefGoogle Scholar
Li, Z. (2011). Measure-Valued Branching Markov Processes. Springer, Heidelberg.CrossRefGoogle Scholar
Li, Z. (2019). Sample paths of continuous-state branching processes with dependent immigration. Stoch. Models 35, 167–196.CrossRefGoogle Scholar
Li, Z., Wang, H. and Xiong, J. (2005). Conditional log-Laplace functionals of immigration superprocesses with dependent spatial motion. Acta Appl. Math. 88, 143–175.CrossRefGoogle Scholar
Li, Z., Wang, H. and Xiong, J. (2008). Conditional entrance laws for superprocesses with dependent spatial motion. Infin. Dimens. Anal. Quantum Prob. Relat. Top. 11, 259–278.CrossRefGoogle Scholar
Li, Z., Wang, H., Xiong, J. and Zhou, X. (2012). Joint continuity of the solutions to a class of nonlinear SPDEs. Prob. Theory Relat. Fields 153, 441–469.CrossRefGoogle Scholar
Mytnik, L. (1996). Superprocesses in random environments. Ann. Prob. 24, 1953–1978.Google Scholar
Mytnik, L. and Xiong, J. (2007). Local extinction for superprocesses in random environments. Electron. J. Prob. 12, 1349–1378.CrossRefGoogle Scholar
Walsh, J. (1986). An introduction to stochastic partial differential equations. In Ecole d’Eté de Probabilités de Saint-Flour XIV – 1984 (Lect. Notes Math. 1180). Springer, Berlin, pp. 256–439.CrossRefGoogle Scholar
Xiong, J. (2004). A stochastic log-Laplace equation. Ann. Prob. 32, 2362–2388.CrossRefGoogle Scholar
Xiong, J. (2004). Long-term behavior for superprocesses over a stochastic flow. Electron. Commun. Prob. 9, 36–52.CrossRefGoogle Scholar
Xiong, J. (2008). An Introduction to Stochastic Filtering Theory. Oxford University Press.CrossRefGoogle Scholar